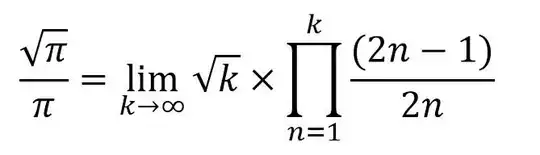Find the limits (without Stirling's approximation ) :
$$\lim_{n}( \frac{1\cdot3\cdot5\cdot \cdot \cdot(2n-1)}{2\cdot4\cdot6 \cdot \cdot \cdot (2n)} ) =?$$
My Try :
$$\frac{1\times 3\times 5\cdots \times(2n-1)}{2\times 4\times 6\cdots \times(2n)}=\frac{(2n)!}{4^n(n!)^2}$$
now what ?
This is $$\prod_{n=1}^\infty\left(1-\frac1{2n}\right).$$ Its logarithm is $$\sum_{n=1}^\infty\left(-\frac1{2n}+O(n^{-2})\right).$$ Does that sum converge/diverge/what?
Use induction to prove that $\frac{(2n)!}{4^n(n!)^2} < \frac{1}{\sqrt{n+1}}$. Now, because $\frac{1}{\sqrt{n+1}}$ tends to 0, it follows that your limit is 0.
maybe it will help you. the answer in the image is a partial result
Since the root of k is necessary for it to converge to a value, I must assume that the limit of the production tends to zero, and that its rate of growth is equal to that of the square root of k
