7

Consider the affine variety with coordinate ring $R=\mathbb{C}[x,y]/(y^2-x^3)$.

It is clear that the coordinate ring $R$ is not integrally closed since $t=y/x$, an element of the corresponding quotient field, is a root of an integral equation.

What is the geometric intuition relating the failure of $y/x$ to belong to $R$ and the cusp we see on the graph of $y^2-x^2=0$?

user7090
  • 5,453
  • 1
  • 22
  • 53
  • To desingularize the curve, one can blow up the origin. Consider the graph $\Gamma$ of the map $f(x,y) = y/x$ defined on $\mathbb{A}^2 \setminus {(0,0)}$, so $\Gamma$ is a subseteq of $\mathbb{A}^2 \times \mathbb{A}^1$. The function $y/x$ gives the slopes of the different tangent lines, and since this is the $z$-coordinate in $\Gamma$, it turns the singularity into a point tangent to the $z$-axis. You can read more in section 7.2 of Fulton, and I may try to give a full answer later. – Viktor Vaughn Nov 17 '17 at 05:03
  • 1
    Maybe helpful: https://mathoverflow.net/questions/1504/what-is-the-geometric-meaning-of-integral-closure. – Zach Teitler Nov 17 '17 at 05:04

2 Answers2

5

The rational function $y/x$ is regular (i.e., defined) at every point on your curve $C$ other than the origin $P = (0,0)$, but at $P$ it is undefined. In order to get a function defined at the origin, we can blow up the point $P$, which will resolve the singularity at $P$.

The idea behind blowing up is the following. At a singular point $P$, there are multiple tangent lines. So we can replace that single point by several points, one for each tangent line, by adding another coordinate (a copy of $\mathbb{P}^1$) that keeps track of the slope of the tangent line. When $P = (0,0)$ is the origin, the slope is given by the function $y/x$, so our new coordinate $z$ will satisfy $z = y/x$, or $y = xz$ if we clear denominators. So really the blowup is (the closure of) the graph of the function $y/x$ on $C \setminus P$; see section 7.2 of Fulton's Algebraic Curves for details.

Your example is a bit confusing since the cuspidal cubic $y^2 = x^3$ has just one tangent line ($y = 0$) with multiplicity $2$ at the origin, so let's first consider the nodal cubic $y^2 = x^2(x + 1)$. Since its homogeneous term of lowest order is $y^2 - x^2 = (y - x)(y + x)$, then the nodal cubic has tangent lines $y = x$ and $y = -x$ at the origin. The function $y/x$ allows us to distinguish between the two branches of the curve. For points along the branch approximated by $y = x$ we have $y/x \approx 1$, and for those on the other branch, we will have $y/x \approx -1$.

So we will "pull apart" these branches by making a curve in $\mathbb{A}^2 \times \mathbb{P}^1$ whose $z$-coordinate is $y/x$. To find the equations for the blowup $\newcommand{\wt}{\widetilde} \wt{C}$, we simply substitute $y = xz$ in to the equations for $C$: \begin{align*} x^2(x+1) &= y^2 = x^2 z^2 \implies 0 = x^2(z^2 - (x+1)) = 0 \end{align*} The factor of $x^2$ corresponds to the extra factor of $\mathbb{P}^1$ we introduced, while the other factor gives us the relation $x = z^2 - 1$. Since $y = xz$, we find the parametric curve $$ \newcommand{\C}{\mathbb{C}} \wt{C} = \{(z^2 - 1, z(z^2 - 1), z) : z \in \C\} \, . $$ Below is the plot (made in SageMath) of the original curve, the blowup, and the points where it intersects the added copy of $\mathbb{P}^1$.

$\hspace{3cm}$ 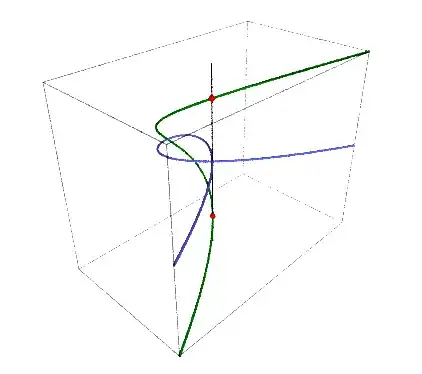enter image description here

We can do the same thing in the case of the cuspidal cubic, obtaining the parametric curve $$ \wt{C} = \{(z^2 , z^3, z) : z \in \C\} $$ as shown in Zach Teitler's answer.

$\hspace{3cm}$ 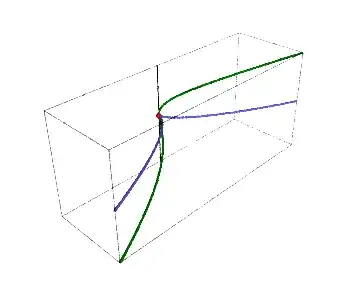enter image description here

It's kind of hard to see what's going on from these still images, so it might be more illuminating to play with the interactive plots (made with SageMathCell) yourself: nodal cubic, cuspidal cubic.

The code for these plots is below.

# nodal cubic
var('t')
p1 = parametric_plot((t^2-1,t*(t^2-1),0), (t,-1.5,1.5), thickness = 2)
p2 = parametric_plot((t^2-1,t*(t^2-1),t), (t,-1.5,1.5), color = "green", thickness = 2)
p3 = parametric_plot((0,0,t), (t,-1.5,1.5), color = "black")
pts = point([(0,0,-1), (0,0,1)], color = "red", size = 5)
show(p1+p2+p3+pts)

# cuspidal cubic
var('t')
p1 = parametric_plot((t^2,t^3,0), (t,-1.5,1.5), thickness = 2)
p2 = parametric_plot((t^2,t^3,t), (t,-1.5,1.5), color = "green", thickness = 2)
p3 = parametric_plot((0,0,t), (t,-1.5,1.5), color = "black")
pts = point([(0,0,0)], color = "red", size = 5)
show(p1+p2+p3+pts)

This paper and this webpage have some great images, too.

Viktor Vaughn
  • 19,278
4

Let $R' = R[y/x]$. We can think of $R \subset R' \subset \operatorname{Frac}(R)$, the field of fractions of $R$.

I claim that $R' \cong \mathbb{C}[t]$. Write $t = y/x \in R'$. In $R'$, $xt=y$, so $x^2 t^2 = y^2 = x^3$. Since $R'$ is an integral domain, $t^2 = x$. And then $t^3 = y$. So (with some hand-waving) $R' = \mathbb{C}[x,y,t]/(y^2-x^3) \cong \mathbb{C}[x,y,t]/(t^2-x,t^3-y) \cong \mathbb{C}[t]$.

If you are familiar with prime spectra of rings, the inclusion $R \subset R'$ gives a map $\operatorname{Spec} R' \to \operatorname{Spec} R$.

If you would rather work with affine varieties, $R = \mathbb{C}[x,y]/(y^2-x^3)$ means $\operatorname{Spec}(R) = V(y^2-x^3)$. What about $R'$? Here $\operatorname{Spec}(R') = V(t^2-x,t^3-y) \subset \mathbb{C}^3$. This is a smooth (nonsingular) curve, parametrized by $t \mapsto (t^2,t^3,t)=(x,y,t)$.

The projection $(x,y,t) \mapsto (x,y)$ gives a map of curves $V(t^2-x,t^3-y) \to V(y^2-x^3)$.

The projection $(x,y,t) \mapsto (x,y)$ has a critical point when the tangent line of the curve is "vertical", i.e., in the kernel of the projection to the $xy$-plane. The derivative of the parametrization is $(2t,3t^2,1)$, which is equal to $(0,0,1)$ when $t=0$. So $t=0$ (or $(x,y,t) = (0,0,0)$) is a critical point of the projection from this curve to the $xy$-plane, and $(x,y)=(0,0)$ is a critical value.

Zach Teitler
  • 3,020