Probability brain teaser with infinite loop

Question

I found this problem and I've been stuck on how to solve it.

A miner is trapped in a mine containing 3 doors. The first door leads to a tunnel that will take him to safety after 3 hours of travel. The second door leads to a tunnel that will return him to the mine after 5 hours of travel. The third door leads to a tunnel that will return him to the mine after 7 hours. If we assume that the miner is at all times equally likely to choose any one of doors, what is the expected length of time until he reaches safety?

The fact that the miner could be stuck in an infinite loop has confused me. Any help is greatly appreciated.

Answer 1

Let $T$ be the time spent in the mine. Conditioning on the first door the miner chooses, we get $$ \mathbb{E}[T]=\frac{1}{3}\cdot3+\frac{1}{3}(5+\mathbb{E}[T])+\frac{1}{3}(7+\mathbb{E}[T])$$ so $$ \mathbb{E}[T]=5+\frac{2}{3}\mathbb{E}[T].$$ If $\mathbb{E}[T]$ is finite, then we can conclude that $\mathbb{E}[T]=15$.

To see that $\mathbb{E}[T]$ is finite, let $X$ be the number of times the miner chooses a door. Then $ \mathbb{P}(X\geq n)=(\frac{2}{3})^{n-1}$ for $n=1,2,3,\dots$, hence $$ \mathbb{E}[X]=\sum_{n=1}^{\infty}\mathbb{P}(X\geq n)=\sum_{n=1}^{\infty}\Big(\frac{2}{3}\Big)^{n-1}<\infty$$ And since $T\leq 7(X-1)+3$, we see that $\mathbb{E}[T]<\infty$ as well.

Answer 2

Let $t$ be the expected time to get out. If he takes the second or third door he returns to the same position as the start, so the expected time after he returns is $t$. Therefore we have $$t=\frac 13(3) + \frac 13(t+5)+\frac 13(t+7)\\\frac 13t=5 \\t=15$$

Answer 3

With probability $1$ he will eventually take the correct door so, $$3*\frac11$$

The wrong doors can be combined, $$ +6*\frac23 $$

and repeated $$ +6*(\frac23)^2 $$

and repeated $$ +6*(\frac23)^3 $$

...

This is can be written as a geometric series

$$3 +\sum (6 * (\frac23)^n)$$

Which is known to simplify to $$ 3+ 4/ (1-\frac23)$$

$$= 3+4*3 $$

$$ = 15$$

---

This result seems to generalize. For $K$ doors with paths length $A,B,C,...N$ if only $A$ leads out and all other doors lead back to the choice you get $$A + \sum(B*(\frac{1}{K})^n) + \sum(C*(\frac{1}{K})^n) + ...\sum(N*(\frac{1}{K})^n)$$

Which becomes $$A+(\frac{\frac BK}{1-\frac1K})+(\frac{\frac CK}{1-\frac1K})+...(\frac{\frac NK}{1-\frac1K}))$$

$$=A +\frac BK * K + \frac CK * K + ...\frac NK * K$$

$$=A+B+C+...N$$

Going randomly is equivalent of taking each door once. Weird.

Answer 4

This is a different approach, using the expected time taken for the miner to pass through $n$ doors.

Let $n$ be the number of doors the miner opens and let $P(T=t)$ be the probability the miner takes $t$ hours to exit. For $n=3$, the sequence of doors the miner opens is one of $(2,2,1),(2,3,1),(3,2,1),(3,3,1)$. These sequences correspond to $P(5+5+3)=\frac{1}{3^3}$, $P(5+7+3)=\frac{2}{3^3}$ and $P(7+7+3)=\frac{1}{3^3}$. The numerator of the second probability is $2$ because there are $2$ ways to have $t=15$. The figure below is a graph of the PMF of P(t).

If the miner passes through $n$ doors, of which $k$ are door-$2$, then he will pass $n-1-k$ times through door-$3$. The $-1$ term accounts for him passing through door-$1$. Then, in general, $P(5k+7(n-1-k)+3)=\frac{1}{3^n}\binom{n-1}{k}$. This is because there is a $\frac{1}{3^n}$ probability of picking each sequence of doors, but $\binom{n-1}{k}$ ways to pick that sequence. The miner can pass through door-$2$ between $0$ and $n-1$ times, so $0\leq k\leq n-1$.

$\mathbb{E}[T]=\sum tP(t)$

At $n$, the expected value, $\mathbb{E}[T]$, is:

$$ \begin{aligned} \mathbb{E}[T]&=\sum _k tP(t) \\ &=\sum_{0\leq k\leq n-1}\frac{5k+7(n-1-k)+3}{3^n}\binom{n-1}{k} \\ &=\frac{1}{3^n}\left[(7n-4)\sum\binom{n-1}{k}-2\sum k\binom{n-1}{k}\right] \\ &=\frac{1}{3^n}\left[2^{n-1}(7n-4)-2^{n-1}(n-1)\right] \\ &=\frac{2^{n-1}(6n+3)}{3^n} \end{aligned} $$

Then, the expected value over all $n$ is:

$$ \begin{aligned} \mathbb{E}[T]&=\sum_{n\in\mathbb{Z^+}} \frac{2^{n-1}(6n+3)}{3^n} \\ &=15 \end{aligned} $$

Answer 5

Consider a simpler example: you have a fair coin. You toss the coin over and over and over again. What is the expected number times that you will toss the coin before you get heads? Of course, it is possible that you will toss the coin infinitely many times and never ever get heads. On the other hand, it is also possible that you will get heads on the very first toss. Hopefully, your intuition is that it is extremely unlikely that you will have to toss the coin more than a few times before it comes up heads. We can summarize the whole process with a tree diagram:

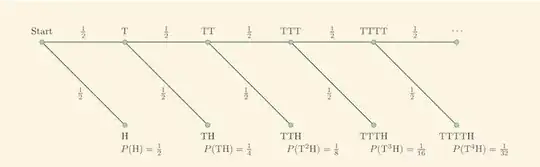
The probability at each leaf is the product of all of the probabilities leading up to it (this is a result of independence; note that these kind of diagrams can often be useful for understanding conditioning). On the top row, we just keep tossing tails over and over and over again. The terminal outcomes all end with heads. Then \begin{align} \mathbb{E}[\text{number of tosses}] &= 1\cdot \mathrm{P}(\mathrm{H}) + 2\cdot \mathrm{P}(\mathrm{TH}) + 3\cdot \mathrm{P}(\mathrm{TTH}) + 4\cdot \mathrm{P}(\mathrm{TTTH}) + \dotsb \\ &= \frac{1}{2} + \frac{2}{4} + \frac{3}{8} + \frac{4}{16} + \dotsb \\ &= \sum_{n=1}^{\infty} \frac{n}{2^n} \\ &= 2. \end{align} Hence, on average, we can expect to toss the coin twice.

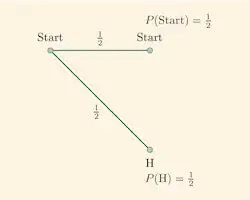
Notice that we can vastly simplify this picture by noting that if we first toss tails, then we go right back to the start. That gives us this picture:

Then \begin{align} \mathbb{E}[\text{number of tosses}] &= 1\cdot \mathrm{P}(\mathrm{H}) + (1+\mathbb{E}[\text{number of tosses}])\cdot \mathrm{P}(\mathrm{T}) \\ &= \frac{1}{2} + \frac{1+\mathbb{E}[\text{number of tosses}]}{2} \end{align} The $1+\mathbb{E}[\text{number of tosses}]$ comes from the fact that if we toss tails on the first coin toss, then we have already tossed the coin once, but everything else is as though we just started the process from the beginning. This can be phrased in terms of conditional probability, but I don't think that the extra notation will help much here. In any even, solving for the expected number of tosses, we get $$ \frac{1}{2} \mathbb{E}[\text{number of tosses}] = 1 \implies \mathbb{E}[\text{number of tosses}] = 2. $$

---

So, what does this have to do with the cave problem? To generalize the above argument to the cave problem first imagine that you are in the room described, and have a fair three sided coin (would it be better if I suggested that you had a d3?). Every time you come back to the start, you toss your three sided coin to decide which door to go through. With probability $\frac{1}{3}$ you go through the 3 hour door and come back to the start, with probability $\frac{1}{3}$ you go through the 5 hour door and escape, and with probability $\frac{1}{3}$ you go through the 7 hour door and come back to the start.

So, suppose that you pick the three hour door first. How long do you expect that you will have to walk altogether? You are going to have to walk for 3 hours, but then you are back to the start. The time that you expect to walk from there is the expected time, which is what we are trying to compute. Therefore if you first go through the three hour door, then you are going to walk $$ 3\text{ hours} + \mathbb{E}[\text{total time}].$$ In other words, using the language of conditional probability (here, it is going to make things a little clearer, I think), we have $$ \mathbb{E}[\text{total time} \mid \text{chose 3 hour door}] = 3 + \mathbb{E}[\text{total time}]. $$

By similar reasoning, we have \begin{align} \mathbb{E}[\text{total time} \mid \text{chose 5 hour door}] &= 5 && (\text{we don't go back to the start}) \\ \mathbb{E}[\text{total time} \mid \text{chose 7 hour door}] &= 7 + \mathbb{E}[\text{total time}] \end{align} Since each of these events is equally likely, we sum in order to get \begin{align} \mathbb{E}[\text{total time}] &= \mathrm{P}(\text{3 hour door}) \cdot (3 + \mathbb{E}[\text{total time}]) + \mathrm{P}(\text{5 hour door})\cdot 5 \\ &\qquad\qquad + \mathrm{P}(\text{7 hour door}) \cdot (7 + \mathbb{E}[\text{total time}]) \\\\ &= \frac{3 + \mathbb{E}[\text{total time}]}{3} + \frac{5}{3} + \frac{7 + \mathbb{E}[\text{total time}]}{3}. \end{align} It remains only to solve for the expected total walking time. To simplify notation, let $E := \mathbb{E}[\text{total time}]$. The above equation reduces to \begin{align} E = \frac{3 + E}{3} + \frac{5}{3} + \frac{7 + E}{3} = \frac{15 + 2E}{3} &\implies \frac{E}{3} = 5 \\ &\implies E = 15. \end{align} In other words, we should expect to travel 15 hours total (which is what the other answers give).

---

The moral of the story here is that traveling for an infinite amount of time is, in principle, possible. However, it is exceedingly unlikely that you will actually travel forever (in fact, you will travel for an infinite amount of time with probability zero—for all practical purposes, it will never happen).

Answer 6

The expected time is the sum of all the times, simply. He can indeed choose any door randomly, and get or not, safe. Hence the expectation is just

$$t = 3 + 5 + 7 = 15$$

Answer 7

Note: this is not a way to solve, but an attempt to provide some intuition for why the miner doesn't get stuck in an infinite loop.

Let's put this in a different light (thanks to Xander Henderson in chatroom for idea):

Each time the miner is looking at the doors, he rolls a dice. If it comes up 1 or 2, he takes door 1. If it comes up 3 or 4, he takes door 2. If it comes up 5 or 6, he takes door 3.

Obviously, the probability is 1/3 for each combination. But it's pretty unlikely he'll get 5 or 6 for all time, or 3 or 4 for all time. It's as possible as flipping a coin and getting heads every time ever - possible, but unlikely. So I'll give an example of me using google's random number generator in place of the miner's die.

First number I got was a 5. (We'll set $t =$ time it takes to get out of the mine.) We add 7 to $t$ and try again. Google now gives me a 3. We add 5 to $t$ (which now equals 12) and go again. This time I got 1 (I swear I'm not making this up). So he's out, and got out in 12 hours. Let's do it again. This time I got 6, 3, 6, 5, 4, 3, 4, 1. That's 7 + 5 + 7 + 7 + 5 + 5 + 5 hours, or 41 hours total. A lot more. Let's do it again. This time I got 6, 1, so 7 hours total.

You can play around more with it, but hopefully what's happening here is clear. We're looking for the expected length of time, kind of like the average. The longer time periods and the shorter time periods "balance out", in a sense. When you flip a coin, you could get all heads for all time, or all tails for all time, but it balances out to a mixture of heads and tails.

So in our case, we simply solve like the other answers have and we get 15 hours; I particularly like Ross Millikan's method for solving.

Answer 8

The fact that the miner could be stuck in an infinite loop has confused me.

using conditional expectation but I still can't understand why the expectation is not infinite

@Xander's answer addresses this point excellently. You expect to flip a coin twice before landing on heads. You might flip any number of tails in a row.

Quoting from an excellent answer for question 4 in the NES/MAA 2017 Collegiate Math Competition:

It is important to remember that the process is memoryless, meaning that the amount of expected time to escape depends only on the miner's current situation and not how many doors the miner has already tried.

Maybe the miner just got there.
Maybe the miner's been there for a year.
He'll be out, on average in 15 hours.

See @Ross' answer for a succinct explanation of the math.

Another intuitive approach:
Consider a cave with $3^n$ miners who all are faced with this same problem. $$3^{n-1} \text{ try door A}$$ $$3^{n-1} \text{ try door B}$$ $$3^{n-1} \text{ try door C}$$

leaving $2\times3^{n-1}$ miners to try again after having walked, on average, 6 hours.

This process is repeated until only $2^n$ miners are left. Now everyone goes home and stops caring about those suckers. How long did the average miner (escaped or still stuck) walk?

\begin{array}{|c|c|c|c|c|c|} \hline n&3^n&|A|\cdot Time& |B+C|\cdot Time & Sum & E(T(n))=\frac{Sum}{Population} \\ \hline 1&3& 1\cdot 3 & 2\cdot 6 & 15 & 5 \\ \hline 2&9& (3+2)\cdot 3 & (6+4)\cdot 6 & 75 & 9.333\\ \hline 3&27& (9+6+4)\cdot 3 & (18+12+8)\cdot 6 &285 & 10.555\\ \hline 4&81& (27+18+12+8)\cdot 3 & (54+36+24+16)\cdot 6 &975 & 12.037\\ \hline \vdots\\ \hline n&3^n& (3^n-2^n)\cdot 3 & 2\cdot (3^n - 2^n)\cdot 6 &15\cdot (3^n - 2^n) & \frac{15\cdot (3^n - 2^n)}{3^n}\\ \hline \end{array}

Now let $n \rightarrow \infty,\text{ and note } \frac{2^n}{3^n}\rightarrow 0$ So for infinitely large groups of miners, the expected time trapped of just escapees and the expected time trapped of everyone will be exactly the same. In other words, $$\lim_{n\rightarrow\infty} E(T(3^n)) = 15\cdot\lim_{n\rightarrow\infty} \frac{3^n-2^n}{3^n}= 15\cdot 1 = 15$$

Answer 9

A probability tree reveals that the miner can expect to spend 9 hours to reach safety. Suppose he chooses Door 7, with probability 1/3; he returns to the start and chooses Door 5 with p = 1/2; he returns and chooses Door 3 with p = 1. Then his path would take take 7 + 5 + 3 = 15 hours with p = (1/3)(1/2)(1) = 1/6. The other possible paths are 7 + 3 = 10, p = 1/6; 5 + 7 + 3 = 15, p = 1/6; 5 + 3 = 8, p = 1/6; and 3, p = 2/6. If T is the rv "time to exit", then its expectation is E(T) = 15*(1/6) + 10*(1/6) + 15*(1/6) + 8*(1/6) + 3*(2/6) = 54/6 = 9 hours.