How to find angle between $2$ points in $3D$ space?

Question

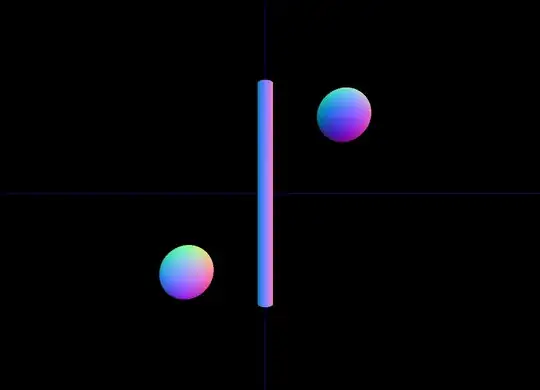
I think I am not able to convey what I need so here is the edited question:

As you can see in the image, a point on the left is at $(-3,-3,0)$ and the point on the right is at $(3,3,0)$.

And when I draw the cylinder it spawns at $(0,0,0)$, the center point of the cylinder is at $(0,0,0)$ and size of the cylinder is the distance between $2$ points. Now my goal is to rotate the cylinder in all $x$, $y$ and $z$-axis so that it connects both the points.

Here this is a $2$D image so I know that I will need to rotate this only in z-axis but I want a generalized for the points anywhere in the coordinate system.

Answer 1

A straightforward way is to use the dot or scalar product of two vectors. $$ \vec{u}\cdot \vec{v} = |\vec{u}||\vec{v}|\cos\theta $$ Here $\theta$ is the angle formed by $\vec{u}$ and $\vec{v}$ when they are tail-to-tail. $\vec{u}\cdot \vec{v}$ is easy to compute using components as $\vec{u}\cdot \vec{v} = u_1v_1 + u_2v_2 + u_3v_3$ so $$\cos\theta = \frac{u_1v_1 + u_2v_2 + u_3v_3}{\sqrt{u_1^2+u_2^2+u_3^2}\sqrt{v_1^2+v_2^2+v_3^2}}\ .$$

In your case you have $$\cos\theta = \frac{1}{\sqrt{3}}\ .$$

---

OK, I'll try to use the above to answer the clarified question:

I will assume that your cylinder spawns with the $z$-axis as the cylinder axis. If this is not true, then you will have to modify what follows. You talk about rotating about all $x$, $y$, and $z$-axis, but actually only two rotations are necessary to rotate a vector that points in the positive $z$-direction to point in an arbitrary direction. Suppose you want to rotate the vector $\vec{k}$ to point in the direction $<a_1,a_2,a_3>$.

By Dmcq (Own work) [CC BY-SA 3.0], via Wikimedia Commons

The angle $\varphi$ is the angle between $\vec{k}$ and $\vec{a}$ and can be found from the above as $$ \varphi = \arccos\left(\frac{a_3}{\sqrt{a_1^2+a_2^2+a_3^2}}\right)$$

The angle $\theta$ is the angle between the positive $x$-axis and the projection of $\vec{a}$ onto the $xy$-plane. $$ \theta = \arccos\left(\frac{<1,0,0>\cdot<a_1,a_2,0>}{|<a_1,a_2,0>|}\right) = \arccos\left(\frac{a_1}{\sqrt{a_1^2+a_2^2}}\right)$$ The expression for $\theta$ is only true if $0\leq\theta\leq 180$. If $\theta >180$ ($y<0$) you will have to patch it up.

Take your cylinder, rotate by $\varphi$ about the $y$-axis (counter-clockwise looking at the $xz$-plane from the positive $y$-axis), then rotate by $\theta$ about the $z$-axis.

Answer 2

Angle between $(a,b,c)$ and $(x,y,z)$ is given by, $$\cos\theta =\frac{ax+by+cz}{\sqrt{a^2+b^2+c^2}\sqrt{x^2+y^2+z^2}}$$

The unit vector from $(a,b,c)$ to $(x,y,z)$ will be$$\frac{a-x}{\sqrt{a^2+b^2+c^2}\sqrt{x^2+y^2+z^2}}i+\frac{b-y}{\sqrt{a^2+b^2+c^2}\sqrt{x^2+y^2+z^2}}j+\frac{c-z}{\sqrt{a^2+b^2+c^2}\sqrt{x^2+y^2+z^2}}k$$ Here the $i^{th}$ term is Cosine of angle with x-axis,

$j^{th}$ term is Cosine of angle with y-axis ,

$k^{th}$ term is Cosine of angle with z-axis.

Answer 3

Samvid,

If the center of the cylinder is at the origin then the axis of the cylinder is a line through the origin: use X=<0,0,0> in my answer above. Still to be determined are r and h.

In other words, suppose that A is a unit vector along the axis of the cylinder. Then we use the same idea as in my previous answer, namely build circles on the axis

cylinder(t,$\alpha$)=t A + r (cos($\alpha$) + sin($\alpha$)) where t $\epsilon$[${-h} \over {2}$,$h \over 2 $] and $\alpha \epsilon [0,2\pi]$

Somehow the other two points must be used to determine r and h and A.

Answer 4

You have two vectors $\mathbf{v}_1$ and $\mathbf{v}_2$ and you want the angle between them. The answer is

$$\theta = \tan^{-1} \left( \frac{\| {\bf v}_1 \times {\bf v}_2 \|}{{\bf v}_1 \cdot {\bf v}_2} \right)$$

In terms of an algorithm see this post with code and an example.

I tent to use the Atan2(y,x) function because it handles the fringe cases better. When the two vectors are perpendicular the methods that rely on Acos() can fail. And the methods that use Asin() fail when the two vectors are parallel.

Answer 5

Samvid

Just so that we are clear: you are working with an application that creates a "generic" cylinder with its center at the origin and you need to move it to some other position in your project. Is this correct?

You also need to change its orientation, right?

How about its height? Can you create it with the correct height or do you need to stretch (or contract) it yourself?

Same for the radius...

If these are all correct, please describe what you know about the "spawned" cylinder.

Answer 6

Two points as vectors: X and Y. The angle between them is the arccos of the ratio of the dot product to the product of the lengths of the vectors:

$\alpha = arccos ({{X.Y} \over {||X|| ||Y||}})$

where ||X|| = $ \sqrt {X.X} $

is the norm (length) of the vector X = $<x_1,x_2,x_3>$

and

V.W = $v_1 w_1+v_2 w_2 + v_3 w_3$

is the usual dot product.

I am not sure that I see what this has to do with your problem, though. How, exactly, is the cylinder determined by the three points (O,X,Y)?

As a guess, suppose that you want a cylinder with the center of the base at X = <1,0,0> and center of the top at Y = <1,1,1> and radius r. Then you would simply determine the line from X to Y (line(t) = t X + (1-t) Y for t $\epsilon [0,1]) $ build a circle around it:

cylinder[t,$ \alpha $] = line[t]+ $ r (cos(\alpha) perp_1 + sin( \alpha ) perp_2 )$ with t $\epsilon$ [0,1] and $\alpha \epsilon$[0,2 $\pi$].

where $perp_1 $ and $perp_2$ are mutually perpendicular unit vectors perpendicular to the line.