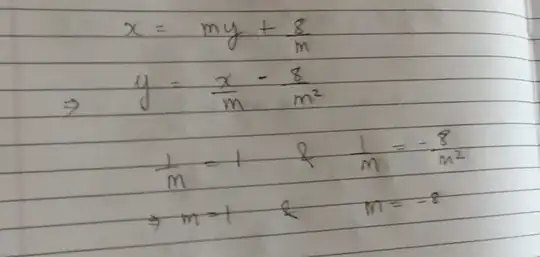I want to find the common tangent to $y^2=4x$ and $x^2=32y$
The equation for a tangent of slope m for each, respectively is: $y=mx+\frac {1}{m}$ and $x=my+\frac{8}{m}$. Since these both represent the same line, I compared the equations but that's giving me a contradictory result. What did I do wrong?
What did I do wrong?
The latter equation $x=my+\frac 8m$ is wrong since the slope of the line $x=my+\frac 8m\iff y=\frac 1mx-\frac{8}{m^2}$ is not $m$.
Replacing $\frac 1m$ with $m$, we see that the latter should be $y=mx-8m^2$.
Comparing this with $y=mx+\frac 1m$, we get $$\frac 1m=-8m^2\implies m=-\frac 12$$
Recall $ax+by=c$ and $Ax+By=C$ represents the same line if and only if $(a,b,c)$ is proportional to $(A,B,C)$. Now the tangent lines to $y^2=4x$ and $x^2=32y$ are $$x = \frac{y_0}{2}y-\frac{y_0^2}{4}\quad\text{and}\quad y = \frac{x_0}{16}x-\frac{x_0^2}{32}$$ that is $$4x -2y_0y=-y_0^2\quad\text{and}\quad 2x_0x-32y = x_0^2.$$ Hence the common tangent can be found by solving $$\frac{4}{2x_0}=\frac{-2y_0}{-32}=\frac{-y_0^2}{x_0^2}$$ and it follows that $x_0=-8$ and $y_0=-4$. Finally the common tangent is $x +2y=-4$.
$$m_1x-m_1^2y-8=0$$
$$m_2^2x-m_2y+1=0$$
will represent the same line iff
$$\dfrac{m_1}{m_2^2}=\dfrac{-m_1^2}{-m_2}=\dfrac{-8}1$$
