11

It occurred to me that functions that are "smooth" but have "infinite slope" may not be considered differentiable at the points where their slope is infinite. An easy example of this is $x^{1/3}$, which is "smooth" in a visual sense (i.e. there are no jumps in the slope, as in a function like $$ f(x) = \begin{cases} x & x\ge 0 \\ 2x & x< 0 \end{cases} $$ which is continuous at the origin but has different slopes as we approach $0$ in different directions), however at the origin the derivative approaches infinity.

So there's a discrepancy, between the intuitive sense of "differentiable" and the mathematically rigorous definition. Intuitively I would like to say yes, $x^{1/3}$ is differentiable at $0$, but mathematically I would be forced to say no because by definition the limit of the newton quotient of this function approaches $\infty$, and so does not exist.

Another example is the function $(xy)^{1/3}$ on $\mathbb{R}^2$. Is this function differentiable on the $x$ and $y$ axes? (with $(x,y)\neq(0,0)$, where it is actually not differentiable) Is there a notion of differentiability that reconciles this discrepancy?

user3002473
  • 8,943
  • 2
    I like this question, because I've never liked the explanation that differentiable and smooth are the same concept. Everyone agrees that the graph of $f(x) = x^3$ is smooth, but for some reason when you reflect it along the diagonal it's suddenly not. This seems contradictory to beginners (and it should be). This is why I teach non-differentiability as coming about in three possibly distinct ways: (1) a point of discontinuity, (2) two competing, non-agreeing tangent lines, or (3) a tangent line which is vertical. (3), of course, handles $g(x) = \sqrt[3]{x}$. – Randall Nov 13 '17 at 16:14
  • 3
    Not only is there a difference between "smooth curve" and"graph of smooth function", there must be such a difference. The notion of "smooth curve" is a geometric one that doesn't depend on introducing a coordinate system in the plane. Another view of this fact is that rigid Euclidean motions send smooth curves to smooth curves. In contrast, the notion of "graph of a smooth function" and even the simpler notion of "graph of a function" do depend on introducing a coordinate system. They are not invariant under rigid motions of the curve (unless you also move the coordinate system). – Andreas Blass Nov 13 '17 at 16:20
  • By the way the intuitive sense of "differentiable" is formed only after learning calculus. Before I studied calculus the word "differentiate" had its usual non mathematical meaning for me. Moreover since this intuitive sense of "differentiable" is based on the study of calculus, I wonder how it can be so different from the definition of a "differentiable" function. – Paramanand Singh Nov 13 '17 at 16:38
  • @AndreasBlass I do like this distinction between smooth curve and smooth graph. It really explains things nicely. I don't think beginning students can get there, but this should be a goal. – Randall Nov 13 '17 at 16:47

3 Answers3

4

The function $x^{1/3}$ is not differentiable at $x=0$, but the graph $\{(x,x^{1/3})\colon x\in\mathbb{R}\}\subseteq \mathbb{R}^2$ is a smooth submanifold, something that for example does not happen with $x^{2/3}$. I believe this latter notion is the one that reconciles your discrepancy.

ziggurism
  • 16,756
2

I would like to tell you why should we consider such functions non-differentible,

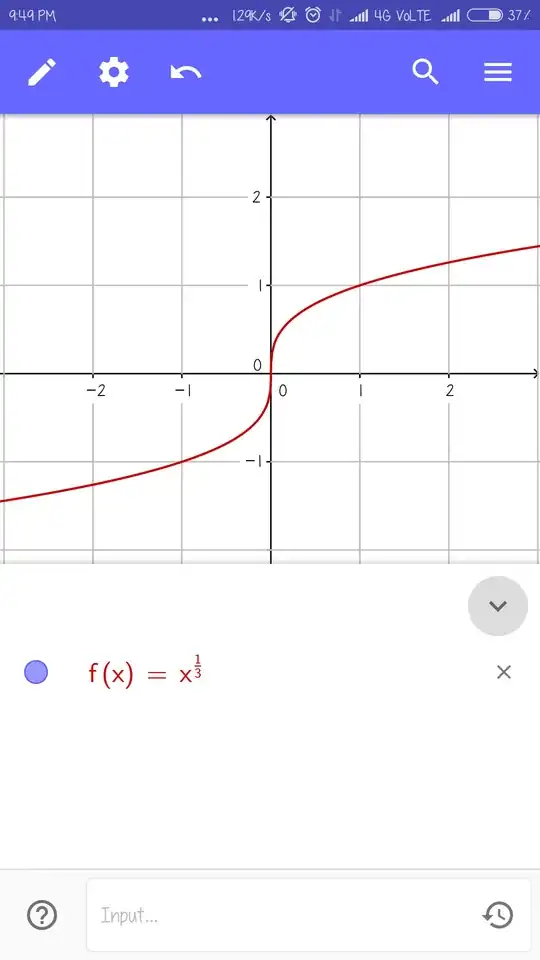For functions whose slope is infinity from the both sides, for eg.,$$x^{\frac{1}{3}}$$ enter image description here Their graphs of derivative appear like this,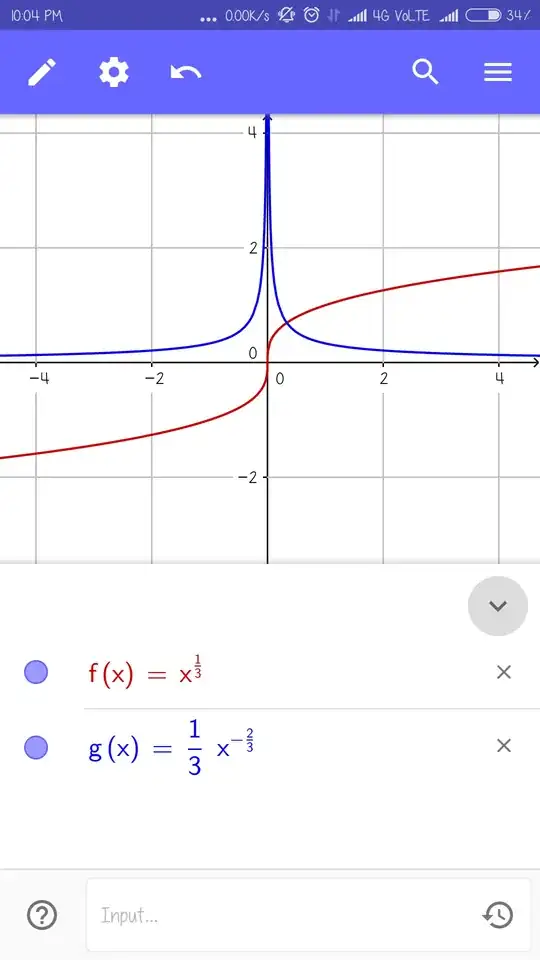enter image description here This gives us a discontinuous function,

That is why we say graph like $x^{\frac{1}{3}}$ are non-differentible at $x=0$

Many of the comments are like ohhh! differentible is not same as smooth But i tend to disagree with this opinion, The guy who discovered this differentiable thing must have done it intuitively and not out of the blue, We must rather than accepting definitions as laws, learn the intuition, this helps in being a better mathematician.

neonpokharkar
  • 1,834
  • That cannot be the graph of the derivative. – Randall Nov 13 '17 at 16:24
  • The derivative is $\frac{1}{3}x^{-\frac{2}{3}}$. It shoots up, not down. – Reinstate Monica Nov 13 '17 at 16:31
  • The coefficient in the derative should be 1/3 – Ovi Nov 13 '17 at 16:31
  • You perhaps claim that $g(x) =f'(x) $ but then you should note that $f'(x) =x^{-2/3}/3$. – Paramanand Singh Nov 13 '17 at 16:32
  • Your idea that if derivative is discontinuous then the function is non-differentiable is not correct. Existence of $f'(a) $ is not dependent on continuity of $f'(x) $ at $a$. – Paramanand Singh Nov 13 '17 at 16:42
  • It mostly is, it is not only when we get oscillating limits in the derivative function – neonpokharkar Nov 13 '17 at 16:50
  • Read this wiki page for more info https://en.m.wikipedia.org/wiki/Differentiable_function @Paramanand Singh – neonpokharkar Nov 13 '17 at 16:57
  • What would you say for functions that are differentiable only at a single point? It does not even make sense to talk of continuity of derivative in such cases. It is best to avoid imprecise ideas which are a major source of confusion for beginners and relatively harmless for the experienced ones. – Paramanand Singh Nov 13 '17 at 16:59
  • Can you name such a function? – neonpokharkar Nov 13 '17 at 17:00
  • One simple example is $f(x) =x^2$ if $x$ is rational and $f(x) =-x^2$ otherwise. This $f$ is continuous only at $0$, differentiable only at $0$ and $f'(0)=0$. – Paramanand Singh Nov 13 '17 at 17:14
  • Well then $$f'(0)$$ is also continuous, check it! – neonpokharkar Nov 13 '17 at 17:17
  • You did not get my point. Derivative $f'$ exists only at point $0$ and not anywhere else. In fact $f$ is continuous only at $0$ and discontinuous at all other points so derivative does not exist at those points. How did you get $2x$ and $-2x$? The example is simple but not as trivial as you are thinking. – Paramanand Singh Nov 13 '17 at 17:23
  • You are right, but the actual graph of f'(0) , if we put it, will be continuous at x=0 @Paramanand Singh – neonpokharkar Nov 13 '17 at 17:41
  • The actual graph of $f'$ will consist of just a single point namely the origin. – Paramanand Singh Nov 13 '17 at 20:21
  • Does the derivative of $ f(x) = x^{1/3} $ exist at $x=0$ on the extended real numbers $ \bar{\mathbb{R}} $ where we define. $ \bar{\mathbb{R}} = \mathbb{R} \cup { \pm \infty } $ – john Aug 26 '18 at 11:15
1

Functions are not differentiable at points where they have infinite slope, and in that respect equating "differentiable" with "smooth" is not perfect.

As far as functions of two or more variables go, a complication is that in some cases they are considered not differentiable at points where not only do the partial derivatives exist, but all directional derivatives exist. For example: $$ f(x,y) = r\sin(2\theta) \text{ where } r = \sqrt{x^2+y^2} \text{ and } x=r\cos\theta \text{ and } y = r\sin\theta. $$ For this function you have $$ \left.\frac{\partial f}{\partial x} \right|_{(x,y)=(0,0)} = 0 \text{ and } \left.\frac{\partial f}{\partial y} \right|_{(x,y)=(0,0)} = 0 \tag 1 $$ and further more the directional derivative in every direction exists, but nonetheless the function is not differentiable at $(0,0).$ The reason is that line $(1)$ above would require the tangent plane to coincide with the $x,y$-plane, but the slope in a direction halfway between the directions of the $x$- and $y$-axes is not $0,$ but $1.$

Michael Hardy
  • 1