how does expectation maximization work?

Question

I'm reading a tutorial on expectation maximization which gives an example of a coin flipping experiment (the description is at http://www.nature.com/nbt/journal/v26/n8/full/nbt1406.html?pagewanted=all). Could you please help me understand where the probabilities in step 2 of the process (i.e. in the middle of part b in the below illustration) come from? Thank you.

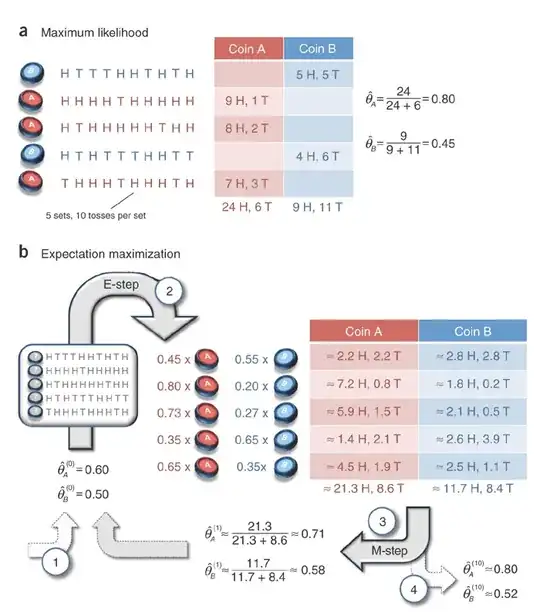
1. EM starts with an initial guess of the parameters. 2. In the E-step, a probability distribution over possible completions is computed using the current parameters. The counts shown in the table are the expected numbers of heads and tails according to this distribution. 3. In the M-step, new parameters are determined using the current completions. 4. After several repetitions of the E-step and M-step, the algorithm converges.

Answer 1

These are the likelihoods of the corresponding set of $10$ coin tosses having been produced by the two coins (using the current estimate for their biases) normalized to add up to $1$. The estimated probability of $k$ out of $10$ tosses of coin $i$ ($i\in\{A,B\}$) yielding heads is

$$p_i(k)=\left({10\atop k}\right) \theta_i^k (1-\theta_i)^{10-k}\;.$$

The binomial coefficient is the same for both coins, so it drops out in the normalization, and only the ratio of the remaining factors determines the result.

For instance, in the second row, we have $9$ heads and $1$ tails. Given the current bias estimates $\theta_A=0.6$ and $\theta_B=0.5$, the factors are

$$\theta_A^9 (1-\theta_A)^{10-9}\simeq0.004$$

and

$$\theta_B^9 (1-\theta_B)^{10-9}\simeq0.001\;,$$

resulting in the numbers

$$\frac{0.004}{0.004+0.001}=0.8$$

and

$$\frac{0.001}{0.004+0.001}=0.2$$

in the second row.

Answer 2

Consider one of the coin-toss realizations in the figure.

Let $P(H_9T_1|A)$ be the probability of observing 9 heads, 1 tail when coin is A.

Let $P(H_9T_1|B)$ be the probability of observing 9 heads, 1 tail when coin is B.

Let $P(A|H_9T_1)$ be the probability of the coin being A when you observe 9 heads, 1 tail.

Let $P(B|H_9T_1)$ be the probability of the coin being B when you observe 9 heads, 1 tail.

Apply conditional probability definition.

$P(A|H_9T_1) = \frac{P(A) \cdot P(H_9T_1|A)}{P(H_9T_1)}$

$P(B|H_9T_1) = \frac{P(B) \cdot P(H_9T_1|B)}{P(H_9T_1)}$

Now,

$P(A) = 0.5 = P(B)$

Estimates of $P(H_9T_1|A)$ and $P(H_9T_1|B)$ are computed using method described by @joriki

Since the coin can either be A or B, $P(A|H_9T_1) + P(B|H_9T_1) = 1$

Hence you can calculate numbers in step 2. They are $P(A|H_9T_1)$ and $P(B|H_9T_1)$ respectively.

Answer 3

In the above picture, the floats indicate how likely the heads are from the coin A or from coin B, provided the lastly estimated $\hat\theta_A$ and $\hat\theta_B$. The crux is that $\hat\theta_A$ and $\hat\theta_B$ are intialized randomly, but if any one of them is not set good enough the likelihood will be correspondingly small and then the other may be large after the following normalization step. And then the expected heads and tails are calcuated using the probability of the 10 flips coming from A or coming from B. Any observation can be from A or from B then the floats are the probabilities of these two conditions. Given the guessed probabilities we can then calculate the new $\hat\theta_A$ and $\hat\theta_B$. If these two parameters are estimated good enough the likelihood would be both high for them(approximate to the true likelihood) and the new parameters would be almost the same as the previous one.

Answer 4

• Let o1 <5H,5T>,o2 <9H,1T>,o3 <8H,2T>,o4 <4H,6T>,o5 <7H,3T> be five observation respectively.
• So each of these observation can either come from coin A with probability 0.5 or from coin B with probability 0.5
• If we select coin A , pA_Head denote the probability of Head from coin A , which is initialized as 0.60
• If we select coin B , pB_Head denote the probability of Head from coin B , which is initialized as 0.50

---

Now we have to find out weather these five observation has come from Coin A or Coin B. i.e we have to find P(A | o2) and P (B | o2) Now, P(A|o1) = P(A,o2) / P(o2)

• o2 can come from either Coin A or Coin B, So P(o2) = P(o2,A) + P(o2,B) [ Sum rule of Probability]
• P(A,o2) = P(A) * P(o2|A)
• P(B,o2) = P(B) * P(o2|B)
• P(o2|A) = (9+1) C 9 * pA_head^(9) * (1-pA_head)^1
• P(o2|B) = (9+1) C 9 * pB_head^(9) * (1-pB_head)^1
• P(A|o2) = [P(A) * 10 C 9 * pA_head^(9) * (1-pA_head)^1 ] / [ {P(A) * 10 C 9 * pA_head^(9) * (1-pA_head)^1 } + {P(B) * 10 C 9 * pB_head^(9) * (1-pB_head)^1 } ]
• Since P(A) = P(B) = 0.5 , Hence P(A|o2) = pA_head^(9) * (1-pA_head)^1 / [ pA_head^(9) * (1-pA_head)^1 + pB_head^(9) * (1-pB_head)^1 } ] = (0.6^9 *0.4 ) / [ (0.6^9 * 0.4^1) + ( 0.50^9 * 0.50^1)]