1

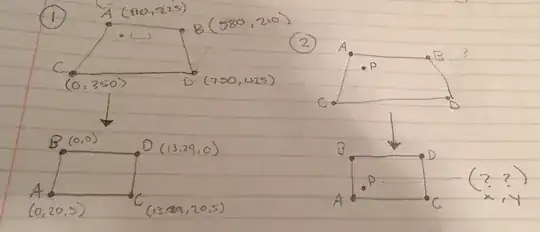
This is for a CS project, however I am having trouble with the linear algebra portion. Based on this reference image:

Reference Image

So in step 1, I am transforming one quadrilateral (let's call it Coordinate System M) to another (let's call it Coordinate System N) and want to find the transformation matrix that makes this possible.

In step 2, I have a new point in Coordinate System M that needs to be mapped to Coordinate System N.

Apologies for not using, perhaps, the right mathematical wording, but linear algebra isn't exactly my strong suit.

Davide Giraudo
  • 172,925
user2646689
  • 13
  • Do you know basis in N and M? –  Nov 08 '17 at 18:06
  • I'm sorry. I'm not sure what you mean by that. – user2646689 Nov 08 '17 at 18:09
  • You don't know what basis is ? –  Nov 08 '17 at 18:13
  • Yes I know the bases of M and N. In your original comment it was a verb and I didn't know what it meant "to basis" something. – user2646689 Nov 08 '17 at 18:16
  • You need to find out how basis vectors of M behave under your coordinate transformation. –  Nov 08 '17 at 18:20
  • Can't I do that by just finding the transformation matrix? – user2646689 Nov 08 '17 at 18:27
  • You need that to find transformation matrix. –  Nov 08 '17 at 18:31
  • AT=B T=A^-1 B That's what I've been rolling with. I know it rotates and scales but I'm not sure how to represent that. – user2646689 Nov 08 '17 at 18:53
  • There are known transformation that rotates and scales. Why can't you use them ? –  Nov 08 '17 at 18:57
  • Because it isn't a perfect rotation and scale. It's mapping an irregular quadrilateral to a rectangle. Note the image I posted – user2646689 Nov 08 '17 at 19:29
  • Ok, can you give a concrete example ? Like with a quadrilateral with known coordinates and coordinats of resultant rectangle. –  Nov 08 '17 at 20:02
  • I've updated the reference image with coordinates – user2646689 Nov 08 '17 at 22:29
  • The most likely reason that you’re having difficulty with this is that you should be looking for a planar perspective transformation instead of a linear transformation of the plane. In general, there is no linear transformation which maps a given quadrilateral to a rectangle, whereas any two convex quads are related by a perspective transformation. (If you work in homogeneous coordinates, then you can pretend that you’re working with a linear transformation of $\mathbb R^3$ to do the computations.) – amd Nov 08 '17 at 23:04

1 Answers1

2

Nonsingular affine (and linear) transformations preserve parallelism, so unless your quadrilateral is a paralellogram, there’s no affine transformation that will map it into a rectangle. On the other hand, every pair of convex quadrilaterals is related by a planar perspective transformation and, given that this is for a CS project, that’s likely what you’re meant to be using. You’ll need to work in homogeneous coordinates to do this, of course.

There’s a built-in function to compute this transformation in most decent computer graphic libraries, but if you need to work it out for yourself, there’s a nice description of how to compute this transformation here. Following that method, solving $$\begin{bmatrix}110&580&0\\225&210&350\\1&1&1\end{bmatrix} \begin{bmatrix}\lambda\\\mu\\\tau\end{bmatrix} = \begin{bmatrix}750\\425\\1\end{bmatrix}$$ and scaling by the result gives $$A=\begin{bmatrix}-286.077 & 1036.077 & 0.0 \\ -585.158 & 375.131 & 635.026 \\ -2.6007 & 1.7863 & 1.8144 \end{bmatrix}.$$ A similar computation for the destination rectangle produces $$B = \begin{bmatrix} 0.0 & 0.0 & 13.29 \\ -20.5 & 0.0 & 20.5 \\ -1.0 & 1.0 & 1.0 \end{bmatrix}$$ and so the required projective transformation is (approximately) $$H = BA^{-1} = \begin{bmatrix} 0.00192 & 0.0603 & -13.78 \\ -0.01636 & 0.01293 & 6.772 \\ 0.0004275 & 0.001709 & -0.04713 \end{bmatrix}.$$ (If you like, you can rescale this matrix without affecting the transformation that it produces by dividing through by the lower-right element to make it $1$.) I encourage you to work this out for yourself and verify that the vertices are mapped as desired. You can then use this matrix to map any other point in the source to the destination.

This transformation is not affine, of course, but as I mentioned in my comment to your question, we can pretend that we’re working in $\mathbb R^3$ instead of the projective plane $\mathbb{RP}^2$ and treat this as it it were a linear transformation, but instead of transforming points to other points, we’re transforming lines through the origin to other lines through the origin.

amd
  • 53,693