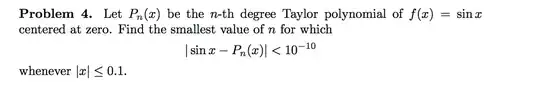1

enter image description here

I'm actually struggling with this question a lot. I've seen a question somewhat similar to it, but I'm not sure if I'm doing this question correctly.

Attempt: My guess is that n should be 11.

$|sinx-(x-x^3/6+x^5/120-x^7/5040+x^9/9!-x^{11}/11!)|$< $|cos(c)/13!|$, for some $c \in (-0.1,0.1)$ Take c to be 0, and we get $<1/13!$, which is less than $10^{-10}$.

I'm not sure if this is correct, nor am I entirely sure what I am doing (I used another question as a reference), or if this is even the correct method. Any help would be much appreciated. Thank you.

Ali
  • 2,277
rain
  • 793

2 Answers2

2

Recall the Lagrange form of the remainder: $$ R_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}x^{n+1}, $$ for some $\xi$ between $0$ and $x$. Since $|f^{(k)}(t)|\leqslant 1$ for all $k$ and $|x|\leqslant\frac1{10}$, we have $$ R_n(x) \leqslant \frac{10^{-(n+1)}}{(n+1)!}, $$ and $$ \frac{10^{-(n+1)}}{(n+1)!}\leqslant 10^{-10} \iff \frac{10^{9-n}}{(n+1)!}\leqslant 1 $$ Let $r_n = \frac{10^{9-n}}{(n+1)!}$. We compute \begin{align} r_5 &= \frac{10^4}{6!} =\frac{125}9>1\\ r_6 &= \frac{10^3}{7!} = \frac{25}{126}<1, \end{align} and hence the desired value of $n$ is $6$.

Math1000
  • 36,983
1

Starting from Math1000's answer and making the problem more general, you want to find $n$ such that $$\frac{10^{-(n+1)}}{(n+1)!}\leqslant 10^{-k} \implies \frac{10^{-p}}{p!}\leqslant 10^{-k} $$ and have a look here for the beautiful solution @robjohn did propose for $\frac{a^n}{n!}\leq 10^{-k}$. Using $a=\frac 1 {10}$ and taking into account that $e^{W(z)}=\frac z{W(z)}$, his formula write $$p\sim \frac{e}{10} \frac x {W(x)}-\frac 12\qquad \text{where}\qquad x=\frac{5 \left(2 k \log (10)+\log \left(\frac{5}{\pi }\right)\right)}{e}$$ For "large" values of $k$,we can approximate the value of Lambert function given here $$W(x)=L_1-L_2+\frac{L_2}{L_1}+\frac{L_2(L_2-2)}{2L_1^2}+\frac{L_2(6-9L_2+2L_2^2)}{6L_1^3}+\cdots$$ where $L_1=\log(x)$ and $L_2=\log(L_1)$.

For different values of $k$, this would give (as real numbers) $$\left( \begin{array}{ccc} k & \text{approximation} & \text{exact} \\ 1 & 0.99678 & 1.00000 \\ 2 & 1.78265 & 1.78210 \\ 3 & 2.48663 & 2.48540 \\ 4 & 3.14418 & 3.14274 \\ 5 & 3.77007 & 3.76856 \\ 6 & 4.37234 & 4.37081 \\ 7 & 4.95599 & 4.95447 \\ 8 & 5.52441 & 5.52292 \\ 9 & 6.08002 & 6.07856 \\ 10 & 6.62464 & 6.62322 \\ 11 & 7.15967 & 7.15829 \\ 12 & 7.68621 & 7.68488 \\ 13 & 8.20518 & 8.20388 \\ 14 & 8.71731 & 8.71605 \\ 15 & 9.22323 & 9.22201 \\ 16 & 9.72346 & 9.72228 \\ 17 & 10.2185 & 10.2173 \\ 18 & 10.7086 & 10.7075 \\ 19 & 11.1943 & 11.1932 \\ 20 & 11.6757 & 11.6747 \end{array} \right)$$ and for $k=10$ the result already given by Math1000.

Claude Leibovici
  • 260,315