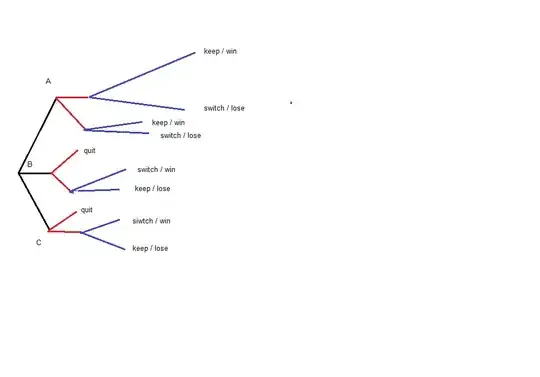
My friend asked me a so called modified version of Monty Hall problem in his opinion. But I find the description a bit spooky and maybe someone here can enlighten us with what is the problem with the description of the problem, or maybe it is me missing something.
Imagine exactly same setting as in monthy hall problem with one difference. Imagine I randomly pick one card. Now, as opposed to the original problem, the show host doesn't know where the car is, and of the remaining two cards, he randomly picks a card: if it happens to be a goat the host shows us this card (as in original game), if it happens to be a car however, my friend said you "quit" the game (or don't consider such case). Now the question is same as in original problem, is it better for me to change my initial choice?
One problem with this description is mainly with the "quit" part. Does not this hinder the process of calculating whether we should switch or not? How do you model the case the host quit the game (in calculating whether you should switch or not)?
He claimed that in such case, switching my initial choice doesn't give me any advantage anymore and made a simulation program as follows. He made 10000 experiments, where he was skipping the part where the host chose a car, so of course he was remained with 2/3 of the experiment test cases, and he claimed that now, since the number of matches the user made (1/3rd of 1000) is half of the number of remaining test cases(2/3rd of 1000- the ones where host didn't choose a car) - it is not advantageous anymore to change the card.
I am failing to find a flaw either in description in problem or in the implementation I mentioned above. Can someone help figure what is wrong with either the problem description or implementation?
I would appreciate some help because I got confused overall with the whole thing now (whereas I understand original monthy hall problem well).
PS. Here is the Java implementation actually: http://codepad.org/rt7fOqei, where he deduces that since match is one half of count, then it makes no sense to change my initial choice.