0

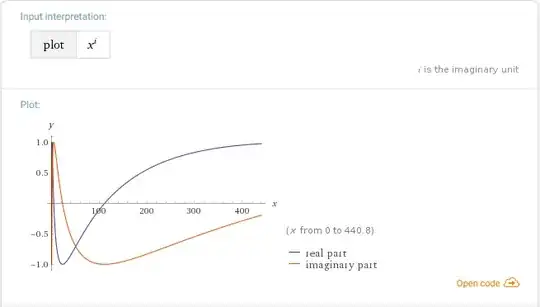
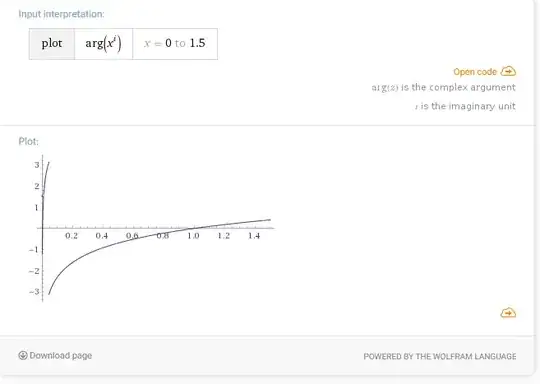
Trying to get more intuition on how exponentiation with complex numbers works, I began entering various functions with complex exponents into WolframAlpha. Both $e^{ix}$ and $i^x$ wasn't all that much of surprise, then I entered $x^i$ and...

plot of x^i

What the heck am I seeing? Supposedly in $e^{\theta i \pi}$ the $e$ is just a scale factor, chosen for convenience, so that argument would remain 1. Meanwhile, as scale factor the base doesn't behave all that nice either...

enter image description here

Could someone explain what's going on here?

Community
  • 1
SF.
  • 1,090
  • I asked a similar question about the behavior of $^{-i}$: https://math.stackexchange.com/q/2416196/471959 it should answer your question – ℋolo Nov 06 '17 at 11:31

1 Answers1

1

By Euler's formula,

$$x^i=e^{i\log x}=\cos(\log x)+i\sin(\log x).$$

The argument is $\log x$, reduced to some $2\pi$ range.

There is no big mystery.

  • And the discontinuity of $arg( x^i )$ around 0.05? Why is it even negative? Or does WolframAlpha's arg mean something else than magnitude? – SF. Nov 06 '17 at 17:42
  • @SF.: I wrote "some $2\pi$ range", not really hard to figure out. –  Nov 06 '17 at 17:43