Confirm that $\int_{0}^{\infty}t^{-1}\sin t dt=\pi/2$.
The guide book I am using gives the following help:
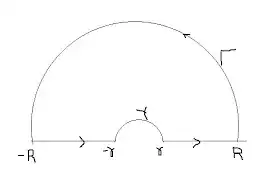
Consider $\int_{\gamma}z^{-1}e^{iz}dz$, where for $0<s<r<\infty$ the contour of integration is described by $\gamma=[s,r]+\gamma_r+[-r,-s]-\gamma_s$, with $\gamma_r(t)=re^{it}$ and $\gamma_s(t)=se^{it}$ on $[0,\pi]$. Recall Exercise IV$.4.20.$
Exercise IV$.4.20.$ For $r$ with $0<r<\infty$ let $I(r)=\int_{\gamma_r}z^{-1}e^{iz}dz$ with $\gamma_r(t)=re^{it}$ on $[0,\pi]$. Show that $I(r)\rightarrow 0$ as $r\rightarrow \infty$ and also that $I(r)\rightarrow \pi i$ as $r\rightarrow 0$
Using the hint, I know that $\int_{\gamma}z^{-1}e^{iz}dz=0$ for the Cauchy theorem, with which $\int_{[s,r]}z^{-1}e^{iz}dz+\int_{\gamma_r}z^{-1}e^{iz}dz+\int_{[-r,-s]}z^{-1}e^{iz}dz-\int_{\gamma_s}z^{-1}e^{iz}dz=0$, but I do not know what else to do here, could someone help me please? Thank you very much.