11

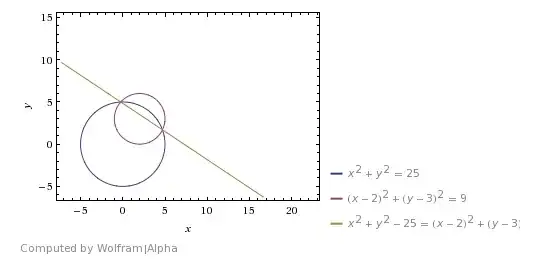
Lets consider the following (random) question:

Find the intersections of the circles $c_1: x^2+y^2=25$ and $c_2: (x-2)^2 + (y-3)^2=9$

In order to solve this we can do $c_2-c_1$, which leaves us with $y=-\dfrac{4}{6}x+\dfrac{29}{6}$.

If we then substitute the $y$ into one of the circles, we get the intersections.

My question, a simple one, is: Why? What does the line $y=-\dfrac{4}{6}x+\dfrac{29}{6}$ represent? Why will we get the intersections if we substitute this particular line in the equation of the circles? Can someone give an intuitive explanation?

JohnPhteven
  • 2,007
  • 1
    Do you mean graphically?Did you draw the graph of the circles and the line you get? – Laura Dec 03 '12 at 15:47
  • Well, my graphing calculator can't graph circles correctly, and certainly not 2 circles and 1 line in 1 image. – JohnPhteven Dec 03 '12 at 15:48
  • 2
    Come on, use ordinary paper, square it yourself if it is not yet squared. Can you say where are the centers and what are the radii? Sorry. Use Wolfram: http://www.wolframalpha.com/input/?i=plot+x%5E2%2By%5E2%3D25%2C+6y%2B4x%3D29 – Berci Dec 03 '12 at 15:51
  • I know the centers and radii of the 2 given circles, of course.. besides, how on earth would I accurately be able to draw the given line on paper, I'm not accurate enough. – JohnPhteven Dec 03 '12 at 15:52
  • Ok so try to draw the two circles.Le line you get is exactly the line crossing both of them an passin trough the intersection so it's clear that you can imagine your point as the intersection between $c1,c2$ but at the same time (and it's easier to calculate) as the intersection between one of them and this line. I'm not sure this is what you mean, so please ask again if it's not clear or you wanted something different. – Laura Dec 03 '12 at 15:52
  • 1
    No need to be perfect but it gives you an idea.Or you can think that the point of intersection are on the circles and their distance from the center is exactly the radius in both case.That line is ortogonal to the one who links the centers and have distance equal to the difference between them.If you think about it,it could help – Laura Dec 03 '12 at 15:58
  • 1
    Whether the circles meet or not, the line is the radical axis of the two circles. – André Nicolas Dec 03 '12 at 17:21

2 Answers2

7

Pictures always help:

enter image description here

The line you obtain is derived, essentially, by expressing each circle as an equation equal to 0 and then equating the circles (which is essentially subtracting the equation of one circle from that of the other) to find the equation of the line $$\mathcal{l}: y=-\dfrac{4}{6}x+\dfrac{29}{6}$$ that passes through the points at which the circles intersect, say $p_1, p_2$. Since there are only two points of intersection, recall that two points define a line, so it is fitting that equation for $\mathcal{l}$ is a line connecting (and passing through) those points. (See the yellowish-brownish line.)

But that line itself doesn't tell us what those points of intersection are.

This line has infinitely many points; to determine which of those points are actually points that the both circles have in common (i.e., to determine the actual points of intersection), we use the equation of the line $\mathcal{l}: y = $ expressed as a function of $x$, and substitute $y$ into either circle's equation. Doing so, we obtain the points on the circles that lie on $\mathcal{l}$ and thus obtain the points $p_1, p_2$where $c_1, c_2$ intersect.

amWhy
  • 209,954
2

Suppose we have some kind of equations $c_1$ and $c_2$ for arbitrary shapes (now circles), using the $2$ coordinate variables $x,y$. Then, if $P=(x_0,y_0)$ is a common point on the two shapes, it means exactly that $c_1(x_0,y_0)$ and $c_2(x_0,y_0)$ are valid statements, consequently so are their sum or any linear combination: $\alpha c_1+\beta c_2$ for $\alpha,\beta\in\Bbb R$.

Now, geometrically what do these linear combinations represent in the original case of circles? It is going to be almost always a circle, but, if $\alpha+\beta=0$, it becomes the equation of a line. But this line still shares the common points of $c_1$ and $c_2$ by the above remark.

Then, what you called 'substitue the line' in one of the original equations, say $c_1$, will give the inteersections of the line and the circle: basically it is just solving the given system of equations.

See also this picture.

Berci
  • 90,745