We've recently come across Bayes Theorem in a lecture. The notes we received are not helpful to me. I have watched a few video tutorials, and I feel like I have an understanding in broad sense and can understand questions attached to said video tutorials, but when it comes to applying the theorem to specific exam questions I'm having difficulty.
The following for example is a question found a past exam paper. I will be sitting a similar exam in a few months time so will recieve a similar questions. However I'm not too sure how to start.
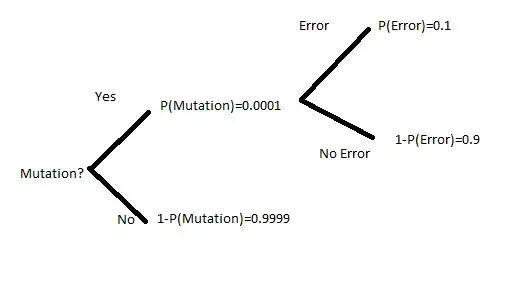
In a fly breeding experiment, it is thought that one in ten thousand flies will exhibit a desired behavioral mutation, within a population of a million. Flies are raised and tested automatically using a robotic flywrangling system. The test for the desired behavioral mutation is very good, with an error rate (in either direction) of only 0.1%. What is the probability that a fly identified by the robot as possessing the desired mutation is actually a target mutant?
Would anyone be able to help me with this problem, please? I am sure if I can work through a worked solution, I won't have difficulty with further questions of this type - they all extremely similar to the above.
Thanks
John