Stronger proof that integration works

Question

So I've been studying integration alongside my class, and the textbook through which we are working contains a very faint reason behind why integration works (nowhere near as rigorous as, for example, why differentiation works) and I was wondering if we could perhaps be shown a stronger proof of why it works.

Here is the proof:

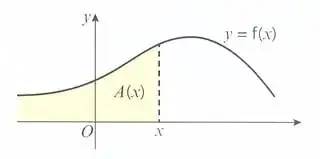
Let $f(x)$ be a function, whose area between the $x$-axis and its curve is given by another function, say $A(x)$, that is

                                           

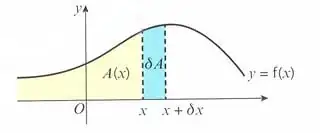
$\implies$ for every increase in $x$, there is a corresponding increase in $A(x)$, denoted by $\delta A$, where $\delta A = A(x+\delta x)-A(x)$, that is

                                               

For infinitesimal increases in $x$, call it $\delta x$, the corresponding increase in $A(x)$ will be $\approx f(x)\delta x$ or $y\delta x$ $$\implies\delta A=y\delta x$$ $$\frac{\delta A}{\delta x}=y$$ $$\frac{A(x+\delta x)-A(x)}{\delta x}=y$$ $$\lim_{\delta x \to 0} \frac{A(x+\delta x)-A(x)}{\delta x} =y$$ $$\frac{dA}{dx}=y$$ $$\therefore A=\int y dx$$

I think the main question is: are there any assumptions that have been made that result in glaring errors? Otherwise are there any errors in general? And if so, any suggested improvements are appreciated, thank you.

Edit: I'm pretty sure the greatest flaw would be assuming that a function describing the area between the curve of a graph and the $x$-axis exists, although I don't see how else this idea would have been conveyed without making this assumption.

Answer 1

What you are talking about is not why integration "works," but rather, one version of the fundamental theorem of calculus. The proof captures the intuition behind the theorem, but it is not rigorous. There are a few problems:

1. Where does the region whose area is labeled $A(x)$ in your figure start? There should be a left edge for the region, say at the vertical line $x=a$. Then the area would be given by a definite integral: \begin{equation} A(x) = \int_a^x f(x)\,dx. \end{equation} (Note: $\int_a^x f(x)\,dx$ is not defined to be $F(x)-F(a)$, where $F$ is an antiderivative of $f$. It is defined as a limit of Riemann sums. The Riemann sums approximate the area, and the limit of the Riemann sums is the exact area. The fundamental theorem of calculus says that $A$ will be an antiderivative of $f$, and that can be used to justify using the formula $F(x)-F(a)$ to compute the integral.)

2. As you point out, one needs to know that $A(x)$ is well-defined--that is, that the Riemann sums in the definition of the definite integral do approach a limit. This is not true for all functions, but it is true as long as $f$ is continuous. This is a difficult theorem, usually proven in more advanced classes. In calculus classes, it is usually just assumed.

3. The proof says that the increase in $A(x)$ will be $\approx f(x)\delta x$, but then it says $\delta A = y\delta x$. How did $\approx$ become =? To make the proof rigorous, you need to say something about how good the approximation is. Here's one way to do it: Let's assume, to simplify things, that $\delta x > 0$, as in your pictures. (Similar reasoning will work for $\delta x < 0$.) Since $f$ is continuous, it has minimum and maximum values on the interval $[x, x+\delta x]$. (This is another fact about continuous functions that is usually stated in calculus classes but only proven in more advanced classes.) Let's say that the minimum is $m$ and the maximum is $M$. This means that there are numbers $c$ and $C$ in the interval $[x,x+\delta x]$ such that $f(c) = m$, $f(C) = M$, and for all other numbers $d$ in that interval, $m \le f(d) \le M$. Now a more precise version of the approximation $\delta A \approx f(x) \delta x$ is: \begin{equation} m \delta x \le \delta A \le M \delta x. \end{equation} Therefore \begin{equation} f(c) = m \le \frac{\delta A}{\delta x} \le M = f(C). \end{equation} Now, to finish the proof, you can use the squeeze theorem. As $\delta x \to 0^+$, $c$ and $C$ both approach $x$, so since $f$ is continuous, $f(c)$ and $f(C)$ both approach $f(x)$. By the squeeze theorem, you get \begin{equation} \lim_{\delta x\to 0^+} \frac{\delta A}{\delta x} = f(x). \end{equation}

Answer 2

Because of the intuitive idea of area, it is unavoidable to assume that $$m(v-u) \le A(v)-A(u) \le M(v-u)$$ if $m$ and $M$ are bounds of $f$ on $[u,v]$, being $a\le u<v\le b$ .

So, since $f$ is continuous, it is easy to show that $A$ is an antiderivative of $f\,$ .

It can be shown that $A$ exists putting $A(x)=\int_a^x f\,$ but there are other ways to show even without using uniform continuity.