$$\{{a_m}+{b_m}:m\geqslant n\}\subseteq \{{a_m}+{b_k}:m,k\geqslant n\}$$
since we are pairing elements from two sets together in the first set while drawing each elements at random from two sets in the second set. By taking the supremum we have:
$$\sup\{{a_m}+{b_m}:m\geqslant n\}\leqslant\sup\{{a_m}+{b_k}:m,k\geqslant n\}\\=\sup\{\{{a_m}:m\geqslant n\}+\sup\{\{{b_m}:m\geqslant n\}$$
Using $\textbf{lemma}$ : $\sup (A+B)=\sup A+ \sup B$ , where $(A+B)=\{a+b:a\in A,b\in B\}$
Taking limit of above iequality gets:
$$\lim_{n\to\infty}\sup\{{a_m}+{b_m}:m\geqslant n\}\leqslant \lim_{n\to\infty}\sup\{{a_m}+{b_k}:m,k\geqslant n\}\\=\lim_{n\to\infty}\sup\{\{{a_m}:m\geqslant n\}+\lim_{n\to\infty} \sup\{\{{b_m}:m\geqslant n\}$$
$$Q.E.D$$
Proof of $\textbf{lemma}$:
$$\forall c\in A+B,\exists a\in A,b\in B,s.t.c=a+b\leqslant \sup A +\sup B$$
So $A+B$ is bounded by $\sup A +\sup B$
$$\forall \varepsilon \gt 0,\exists a \in A,b \in B ,s.t.a \gt \sup A-\varepsilon ,b \gt \sup B -\varepsilon ,a+b\gt \sup A +\sup B -2\varepsilon$$
So any number less than $\sup A +\sup B $ is not an upper bound. Thus $\sup A +\sup B $ is the least upper bound.
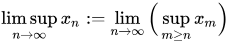
\limsuprather than\lim\supor\mbox{limsup}. – Asaf Karagila Dec 02 '12 at 15:50