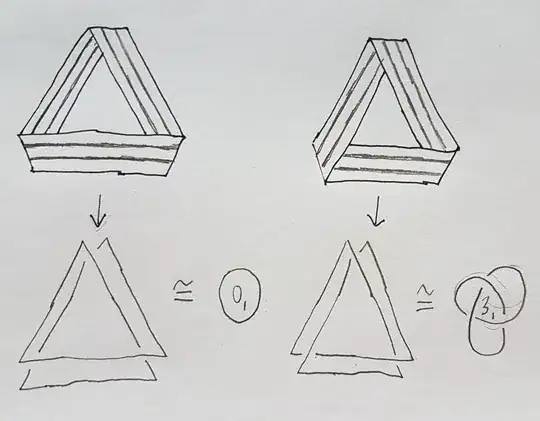
Cutting a multiple twisted Möbius strip in half

Question

At my workplace in the weekends we ususally play around with science and younger children. This months topic in mathemathics was a bit of soft topology. We of course made Möbius strips. What we called $\mathbf{a \ twist}$ was a $180^{\circ}$ rotation of the end of the strip before glueing. So $0$ twist is a ring of paper, $1$ twist gives the Möbius strip $2$ strips gives again an orientable surface (basically the ring "going around twice") and so on. I just wanted to clarify our terminology. After we understood what the word orientable means we of course started to cut the strips in half. The ring, cut along the centerline gave two similar rings, the Möbius strip gave a longer $4$ times twisted strip which is orientable. We understood why this happened (that is where the seemingly extra $3$ twists are coming from and why it resulted in one longer, connected strip). Some started cutting this again and we saw that we got two linked orientable surfaces. We also tried to cut the Möbius strip a bit off from the centerline and understood the result and why are the two resulting strips are linked. One thing we could't wrap our heads around is why, the $3$ times twisted strip ended up having a knot (a usual overhead knot)? We tried $5$ times twisted ones as well and we got more interesting looking knots on the strip.

I learned some undergraduate level topology at university but I have a hard time connecting that knowledge to this phenomena. I searched a bit here at MSE and found really helpful information altough nothing about this "knot story".

Could anyone explain this to me to some extent? Or could anyone give me some links maybe where I can find information about this? Generally I would be really happy to find some scientific description about this whole "cutting the Möbius strip". What operation is a cut for example?

If you have a parametrization of the (generalized) Möbius strip (as in this one), "cutting" is just a matter of appropriately restricting the parameter ranges. You might find the parametric equations here to be useful. — J. M. ain't a mathematician, Oct 23 '17 at 07:31

score 6 · Accepted Answer · answered Oct 23 '17 at 08:17

6

Suppose that the strip, on both of its sides, has two stripes on either side of the centre line. After folding up and cutting along the centre line, treat the stripe(s) as a knotted rope (or ropes).

For the regular Möbius strip (left), the resulting rope can be deformed to a simple ring. For the three-twist Möbius strip (right), a trefoil (overhand) knot results. For a five-twist Möbius strip, the cinquefoil (double overhand) knot is obtained, and so on.

In general, a strip with $n$ twists when cut along the centre line yields the $(n,2)$ torus knot/link. The cut gives one strip if $n$ is odd and two if $n$ is even; as examples of the latter, the two-twist strip (the result of cutting the one-twist strip) when cut yields the Hopf link (two linked rings), while the four-twist strip when cut yields Solomon's link, distinct from the Hopf link.

answered Oct 23 '17 at 08:17

Parcly Taxel

103,344

Wow! Thank you! Too bad I can only give one up vote for this. – Vinyl_cape_jawa Oct 23 '17 at 08:21
@Vinyl_coat_jawa But you can also accept the answer, since you asked the question ;) – Parcly Taxel Oct 23 '17 at 08:21
of course, if I accept the answer won't it get "closed" or something? I mean you definitely answered my question in an really cool way but maybe some others have some other thoughts. – Vinyl_cape_jawa Oct 23 '17 at 08:33
@Vinyl_coat_jawa Don't worry. It won't get closed. Others can still add answers if they want. – Parcly Taxel Oct 23 '17 at 08:33
could you reccomend any books or links about this topic? – Vinyl_cape_jawa Oct 23 '17 at 08:35
@Vinyl_coat_jawa Just search "knot theory". Knot theory is in turn very intricately linked with topology. – Parcly Taxel Oct 23 '17 at 08:36

Cutting a multiple twisted Möbius strip in half

1 Answers1