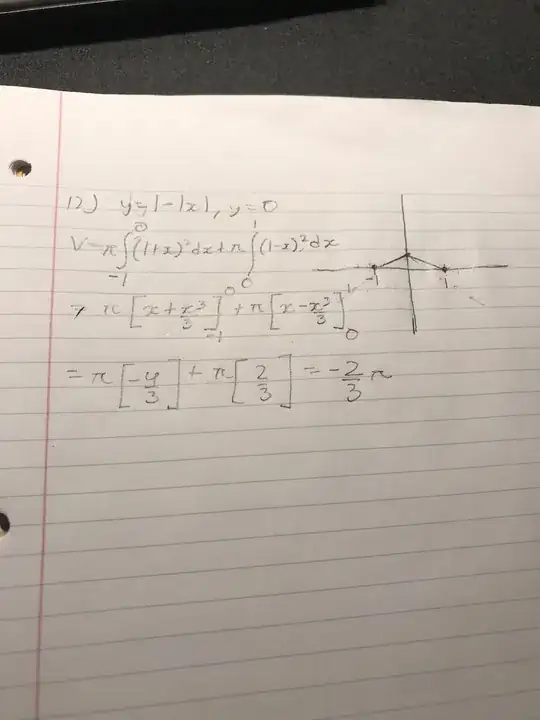Revolution about $x$-axis Error

Question

Can someone please explain to me where my error is in this problem because i should not be getting a negative volume.

Find the volume of the solid generating by revolving this region about the x-axis

$$y= 1 - |x|, y=0. $$

I have attached my work, but I just don't understand how I'm getting a negative answer Revolution Question

$(1-x)^2=(1-x)(1-x)=1-2x+x^2$, again last term: $+x^2$ – imranfat Oct 23 '17 at 01:20 — imranfat, Oct 23 '17 at 01:20
Never mind I was able to get the answer – Hritik Oct 23 '17 at 02:52 — Hritik, Oct 23 '17 at 02:52

score 1 · Answer 1 · edited Oct 23 '17 at 02:00

The integration is wrong.

For example, note that $(1+x)^2=1+\color{blue}{2x}+x^2$ and in general we do not have $(1+x)^2=1+x^2$.

Alternatively, to avoid expansion of the quadratic term, we can also do the following: $$\int_{-1}^0 (1+x)^2 \,dx= \left.\frac{(1+x)^3}{3}\right|_{x=-1}^{x=0}=\frac13$$

Also, by symmetry, the volume generated on the left of $x$-axis is equal to the volume generatd on the right.

Notice that one can also solve this problem (verify your solution) by using formula of volume of cone.

Revolution about $x$-axis Error

1 Answers1