0

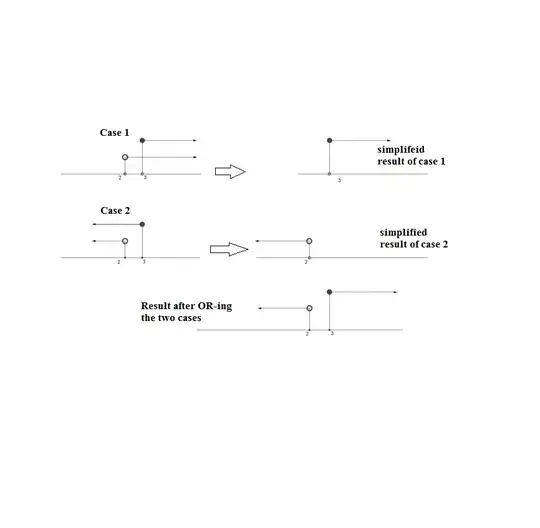
I'm tasked to prove the above implication. However, as this implication has the general form of $P \implies (Q \lor R)$, it's equivalent to $(P \land \neg Q) \implies R$ where

$P:\frac{x}{(x-2)} \leq 3$,

$Q: x<2$ and

$R:x\geq 3$ .

We've used this logical equivalence extensively throughout the chapter, so I'm guessing we should also apply it here. I can't figure out how though.

If I use $(P \land \neg Q) \implies R$, I run into a problem. Assuming the antecedent, $(P \land \neg Q)$, and laying down the foundation of a possible proof, I get:

"Suppose that $\frac{x}{(x-2)} \leq 3$ and $x\geq 2$"

...which is a wrong start, considering $x\geq 2$ can't possibly be correct since that would mean that $x-2$ could amount to zero, and then I wouldn't be able to multiply both sides by $(x-2)$.

How do I go about proving this?

Ius Klesar
  • 1,406

4 Answers4

1

write the inequality in the form $$0\le 3-\frac{x}{x-2}=2\frac{x-3}{x-2}$$ thus we have $$x\geq 3$$ or $$x<2$$

Dr. Sonnhard Graubner
  • 95,283
1

I will limit this answer to addressing the conceptual error in saying "$x\ge2$ can't possibly be correct since that would mean that $x−2$ could amount to zero."

For each value of $x$, the statement "${x\over x-2}\le3$ and $x\ge2$" is either True or False. When you suppose that statement, you are limiting yourself to values of $x$ for which it is True. In order for an "and" statement to be true, both parts of it must be True. Now "$x\ge2$" is certainly True for $x=2$. But the statement "${x\over x-2}\le3$" is not True. To see why not, it helps to state it more fully, with an emphasis on the part that's not true: "The result of dividing the number $x$ by the number $x-2$ is a number that is less than or equal to $3$."

Once you understand that "${x\over x-2}\le3$ and $x\ge2$" implies $x\gt2$, so that $x-2\gt0$, you are free to multiply both sides of ${x\over x-2}\le3$ by $x-2$, getting $x\le3x-6$, which reduces to $3\le x$.

Barry Cipra
  • 79,832
  • That is actually very insightful, but it still doesn't quite jive with my intuition. So if I start off by supposing $\frac{x}{x-2} \leq 3 \land x \geq 2$ , I can then follow this up by saying "because $\frac{x}{x-2}$ is undefined for $x=2$, this statement is equivalent to supposing $\frac{x}{x-2} \leq 3 \land x > 2$" and then work from there? – Ius Klesar Oct 22 '17 at 16:13
  • @IusKlesar, yes. – Barry Cipra Oct 22 '17 at 16:30
  • But then, in calculus I always learned that saying $\frac{1}{x} \geq 0$ is definitely not the same as $\frac{1}{x} >0$, and that one was correct and the other wasn't. Assuming you're correct, wouldn't that make the $\geq$ sign useless, as it's a disjunctive form and therefore only one of its components needs to be true? – Ius Klesar Oct 22 '17 at 16:44
  • @IusKlesar, if $0$ is not in the range of a function $f$, then, for all $x$ in the domain of $f$, the assertion $f(x)\ge0$ is equivalent to the assertion $f(x)\gt0$. But if $0$ is in the range, the two assertions are not equivalent. – Barry Cipra Oct 22 '17 at 16:55
  • @IusKlesar Re: your last comment, for positive $x,$ the statements $\frac1x\ge0$ and $\frac10\ne5$ both could be either true or non-meaningful, depending on how one frames/argues it. – ryang Jun 05 '23 at 13:29
0

Assume that $\frac{x}{x-2} \leq 3$ then $\frac{x-3x+6}{(x-2)} \leq 0$ then $\frac{-2x+6}{x-2} \leq 0$ then $\frac{-2(x-3)}{(x-2)} \leq 0$, then $\frac{x-3}{x-2} \geq 0$ then $(x-2)(x-3) \geq 0$ with $x \not =2$ (the sign of $\frac{a}{b}$ is the same as the sign of $ab$ when $b \not = 0$.) so $(x \geq 3$ or $x \leq 2)$ and $x \not =2$ and hence $x \geq 3$ or $x <2$

mich95
  • 8,713
0

Case 1, when $x \gt 2$, we have $$x \le 3(x – 2)$$ and this gives $$x \ge 3$$ AND-ing the conditions together (See diagram below), we get $x \ge 3$.

OR

Case 2, when $x \lt 2$, we have $$x \ge 3(x – 2)$$ and this gives $$x \le 3$$ AND-ing the conditions together (See diagram below), we get $x \lt 2$.

enter image description here

Result follows after we combine the two cases using ‘OR’.

Mick
  • 17,141