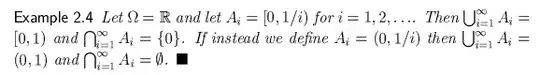Intersection of sets within space [0,1/i] vs (0,1/i) as i approaches infinity

Question

Here's an example from All of Statistics by Wasserman

So when A includes 0, the intersection is just 0, but when it only approaches 0, the intersection is the empty set.

Why is this? Is there a name to describe this property, so I can read more about it? I can visualize why, but I'd like to know the formal terms to describe it.

From the title of your question, perhaps you are looking for the statement that the "infinite intersection of nested non-empty closed subsets of a compact space is not empty" or something similar involving nested bounded closed sets for $\bigcap_i \left[0,\frac1i \right] \not = \emptyset$. Meanwhile $\left(0,\frac1i \right)$ is not closed so does not have this property — Henry, Oct 21 '17 at 23:43

score 0 · Answer 1 · answered Oct 21 '17 at 02:47

In the second case, for any positive number $x$ pick an $i>\frac{1}{x}$. Then it will follow that $\frac{1}{i}<x$ so $x$ cannot lie in the intersection since in does not lie in $\left(0,\frac{1}{i}\right)$. So no positive number lies in the intersection.

In the first case, $0$ lies in each set, so it lies in the intersection. But by the argument above, no positive $x$ can lie in the intersection.

Intersection of sets within space [0,1/i] vs (0,1/i) as i approaches infinity

1 Answers1

Linked