I'm looking for a power of 3 close to a power of 2.
Let's say, what is $(n,m)$ such that $$\left|\frac{2^n}{3^m}-1\right| = \min\left \{\left|\frac{2^i}{3^j}-1 \right|, 1\leq i,j\leq 20\right\} \quad ?$$
The idea is to understand the intervals between musical notes. Any link on this subject is welcomed (I don't know music theory but I'm interested).
You want $2^i \approx 3^j$ with $i,j \in \mathbb N$
(preferably $1 \leq i,j \leq 20$).
Take the logarithm (in any base) of both sides: $$i \log(2) \approx j \log(3).$$
Thus the issue is now to obtain a good rational approximation
$$\underbrace{\dfrac{\log(3)}{\log(2)}}_{N}\approx \dfrac{i}{j}$$
Such rational approximations are obtained as the so-called "convergents" of the continued fraction expansion of number $N$ (https://en.wikipedia.org/wiki/Continued_fraction):
$$N=a_0+\tfrac{1}{a_1+\tfrac{1}{{a_2+\tfrac{1}{\cdots}}}}$$
with $(a_0; a_1, a_3, \cdots )=(1;1,1,2,2,3,1,5,2,23,2,2,1,55,1,...).$
with successive convergents:
$$ i/j = 3/2, \ 5/3, \ 8/5, \ 11/7, \ 19/12, \ 46/29, \ 65/41, \ 84/53, ...$$
$$317/200,\ 401/253, \ 485/306, \ 569/359, \ 1054/665...$$
(that can be found in (https://oeis.org/A254351/internal)).
Good convergents are obtained by (in plain terms) "stopping just before a big $a_k$".
If the "big $a_k$" (!) is 3, one gets :
$$\dfrac{19}{12} \approx 1.5833 \ \ \ \text{of} \ \ \ N = 1.5850...$$
Thus a good tradeoff is to take $i=19$ and $j=12$.
This is connected to the "Pythagorician comma". (https://en.wikipedia.org/wiki/Pythagorean_comma).
Very related : (http://www.math.uwaterloo.ca/~mrubinst/tuning/12.html)
Here I have written different things in different parts; the first and third are related to each other:
Irrelevant to the main question (For those who are interested in the connection between music theory and powers of primes): Years ago when I was writing this answer, I did not know about its connection with music theory. This morning I received a notification for an up-vote to this question (That's why I added this information). 3 or 4 months ago, I got information about the relationship between music theory (Superparticular ratios) and prime powers $2$, $3$, etc.; the links to which I will briefly share here:
ABC, High Quality Commas, and Epimericity (The original link has expired)
Just read the first link (I mean Størmer's theorem), to understand the connection between music theory (Superparticular ratios and ...) and the powers of prime numbers through Pell equations.
Also, you can see the contents of the link in the "Internet Web Archive" in the image below (just to be sure, if this link becomes unavailable in the future):
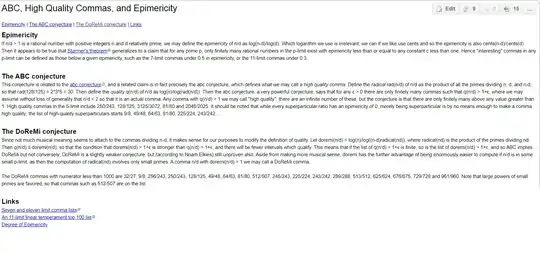
(I still do not even understand why, in the question, why we consider the upper limit to be $20$? and set this restriction? Perhaps for a practical exercise?)
Related to the main question:
Lemma:
Let $\alpha, \beta$ be linearly independent
over rationals $\mathbb{Q}$;
i.e. $\dfrac{\alpha}{\beta} \notin \mathbb{Q}$.
Then the group generated by $\alpha, \beta$ is dense in $\mathbb{Q}$;
i.e.
$
\{ i\alpha+j\beta \ | \ i,j \in \mathbb{Z} \} =
\{ i\alpha-j\beta \ | \ i,j \in \mathbb{Z} \}
$
is dense in $\mathbb{Q}$.
Now let $\alpha:=\log2$ and $\beta:=\log3$,
note that
$\dfrac{\beta}{\alpha}=\dfrac{\log3}{\log2}=\log_23 \notin \mathbb{Q}$;
so if we let $i, j$ varies arbitrary in $\mathbb{N}$,
then
the phrase $i\alpha-j\beta$
will become as small as we want;
i.e. in more mathematical discipline we can say:
for every $0 < \delta \in \mathbb{R}$
there exist $i, j \in \mathbb{N}$
such that $0 < i\alpha-j\beta < \delta$.
Note that: $$ 10^{i\alpha-j\beta}= \dfrac{10^{i\alpha}}{10^{j\beta}}= \dfrac{(10^{\alpha})^{i}}{(10^{\beta})^{j}}= \dfrac{2^i}{3^j} $$
So we can conclude that:
for every $0 < \epsilon \in \mathbb{R}$
there exist $i, j \in \mathbb{N}$
such that $1 < \dfrac{2^i}{3^j} < 1+ \epsilon$.
So ignoring some mathematical disciplines we can say:
if we let $i, j$ varies arbitrary in $\mathbb{N}$,
then
the phrase $\dfrac{2^i}{3^j}$
will become as close to $1$ as we want.
We can restase some similar facts about
$-\delta < i\alpha-j\beta < 0$ and
$-\delta < i\alpha-j\beta < \delta$;
also for
$1- \epsilon < \dfrac{2^i}{3^j} < 1$ and
$1- \epsilon < \dfrac{2^i}{3^j} < 1+ \epsilon$; but it does not matters.
I have seen this problem before:
unsolved problems in number theory by Richard K. Guy;
$F$(None of the above);
$F23$(Small differences between powers of $2$ and $3$.) :
Problem $1$ of Littlewood's book
asks how small $3^n — 2^m$ can be in comparison with $2^m$.
He gives as an example
$$
\dfrac{3^{12}} {2^{19}} = 1+
\dfrac{ 7153 } {524288} \approx 1+
\dfrac{ 1 } { 73 }
\qquad
\text{ (the ratio of } D^{\sharp} \text{ to } E^{\flat}).
$$
[Where $\sharp$ and $\flat$ stands for dièse and Bémol.]
The first few convergents to the continued fraction (see $F20$) $$ log_23= 1+\tfrac{1} {1+\tfrac{1} {1+\tfrac{1} {2+\tfrac{1} {2+\tfrac{1} {3+\tfrac{1} {1+\tfrac{1} {\cdots} } } } } } } $$
for $\log 3$ to the base $2$ are:
$$
\dfrac{ 1}{ 1},
\dfrac{ 2}{ 1},
\dfrac{ 3}{ 2},
\dfrac{ 8}{ 5},
\dfrac{19}{12},
\dfrac{65}{41},
\dfrac{84}{53},
\dots
$$
so Victor Meally observed that
the $\color{Blue}{\text{octave}}$ may conveniently be partitioned
into $12$, $41$ or $53$ intervals,
and that the system of temperament with $53$ degrees
is due to Nicolaus Mercator
($1620-1687$; not Gerhardus, $1512-1594$, of map projection fame).
Ellison used the Gel'fond-Baker method to show that
$$ |2^x-3^y| > 2^x e^{\dfrac{-x}{10}} \qquad \text{for} \qquad x > 27 $$
and Tijdeman used it to show that there is a $c \geq 1$ such that $2^x - 3^y > \dfrac{2^x}{x^c}$.
Croft asks the corresponding question for $n! — 2^m$. $ \ \ \cdots$
That was the exact text from the book, note that the pair $(m,n)$ has been used in the reversed order in that book versus this question has been asked in this site!
At the end of section $F23$; there are four refrences as follows:
F. Beukers, Fractional parts of powers of rationals, Math. Proc. Cambridge Philos. Soc., $90(1981) 13-20$; MR $83$g:$10028$.
A. K. Dubitskas, A lower bound on the value of $||(3/2)^k||$ (Russian), Uspekhi Mat. Nauk, $45(1990) 153-154$; translated in Russian Math. Surveys, $45(1990) 163-164$; MR $91$k:$11058$.
W. J. Ellison, Recipes for solving diophantine problems by Baker's method, S6m. Thiorie Nombms, $1970-71$, Exp. No. $11$, C.N.R.S. Talence, $1971$.
R. Tijdeman, On integers with many small factors, Compositio Math., $26 (1973) 319-330$.
I have found an article by Kurt Mahler with the same name as the first one here.
Also in page $14$ of this paper of Michel Waldschmidt; you can find something.
The continued fraction for $\frac{\log(3)}{\log(2)}$ is $$ 1;1,1,2,2,3,1,5,2,23,2,2,1,1,55,1,4,3,1,1,\dots $$ The convergents are $$ \frac11,\frac21,\frac32,\frac85,\frac{19}{12},\frac{65}{41},\frac{84}{53},\frac{485}{306},\frac{1054}{665},\frac{24727}{15601},\frac{50508}{31867},\frac{125743}{79335},\frac{176251}{111202},\frac{301994}{190537},\frac{16785921}{10590737},\frac{17087915}{10781274},\frac{85137581}{53715833}, \frac{272500658}{171928773},\frac{357638239}{225644606}, \frac{630138897}{397573379},\cdots $$ This gives a number of "close" approximations. For example, the best with exponents between $1$ and $20$, is $$ \left|\frac{2^{19}}{3^{12}}-1\right|=0.01345963145485576 $$ This gives the approximation $2^{19/12}=2.9966$. Since their are $12$ half-steps to the octave, this approximation is very useful.
