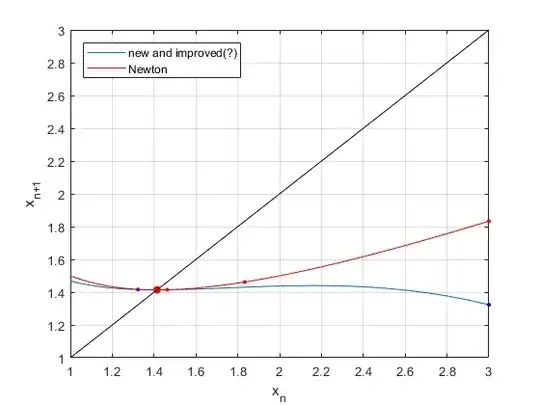
It is well known that the iteration scheme
$$ x_{n+1} = \frac{1}{2} (x_n + \frac{2}{x_n })$$
converges to $\sqrt{2}$ very fast. More precisely, it converges quadratically. The problem is, is there any even faster algorithm? Namely, can we find another polynomial $P(x, 1/x)$ of $x$ and $1/x$ with rational coefficients, such that the iteration scheme
$$x_{n+1} = P \left(x_n , \frac{1}{x_n} \right)$$
converges even faster?
The conjecture is that no such algorithm exists. But I have no idea how to prove it.