Simple bijection $\mathbb N_0 \times \mathbb N_0 \to \mathbb N_0$

Question

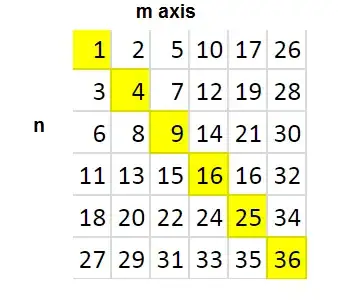
I'm looking for a 'simple' bijection $$ \pi \colon \mathbb N_0 \times \mathbb N_0 \to \mathbb N_0, $$

where 'simple' in this context means that it should be as easy as possible to define and it should be self-evident that said function is in fact a bijection. It's a quest for convenience - not minimal complexity in any rigorous sense.

Here are a couple of examples I came up with - none of which satisfy both requirements:

1. Let $\pi(m,n) = c(2^m3^{n+1})$, where $c \colon \{2^m3^{n+1} \mid m,n \in \mathbb N_0 \}\to \mathbb N_0$ is the order isomorphism (or in fact Mostowski collapse) of its domain under the natural ordering,
2. Let $\pi(m,n) = \langle n,m \rangle$ - Gödel's pairing function,
3. Let $\pi(m,n) = m \oplus n$ - the number resulting from 'riffling' $m,n$ (where we imagine both $m$ and $n$ as in infinite decks of cards whose $i$th element is labeled with its respective $i$th digit).
4. ...

Answer 1

$$\pi(n,m)=2^n(2m+1)-1$$

Break each natural number to a maximal even part, and an odd part. The $-1$ is there for getting $0$ into the fold.

Answer 2

The following (ugly, sorry) picture shows the desired map.

Answer 3

Not sure if this will fit, but it is an explicit arithmetic formula. It is called the Cantor pairing function:

$$C(m,n)=\frac{(m+n)(m+n+1)}{2}+m$$

It is however not obvious that it works. But you can find a proof here.

Answer 4

Asaf was interested in seeing an explicit formula for user469689's picture answer. It can be done following the algorithm described in theorem 1 on Cantor's Pairing Function (see here), but it would look messy with 'odd/even' cases since the picture describes a 'connected path'. So we choose a slightly different path but one that highlights the same 'geometry':

$(0,0) \to$
$(1,0) \to (1,1) \to (0,1) \to $
$(2,0) \to (2,1) \to (2,2) \to (1,2) \to (0,2) \to $
$(3,0) \to (3,1) \to (3,2) \to (3,3) \to (2,3) \to (1,3) \to (0,3) \to $
$\text{etc.} \qquad \text{Figure 1}$

Here is the mapping:

$$ \pi(m,n) = \left\{\begin{array}{lr} n^2+2n-m, & \text{for } m \le n\\ m^2+n, & \text{for } m \gt n \end{array}\right\} $$

As a check, apply $\pi$ to Figure 1:

$\pi(0,0) = 0$
$\pi(1,0)=1 \; \; \pi (1,1)=2 \; \; \pi (0,1)=3$
$\pi(2,0)=4 \; \; \pi (2,1)=5 \; \; \pi (2,2)=6 \; \; \pi (1,2)=7 \; \; \pi (0,2)=8 $
$\pi(3,0)=9 \; \; \pi (3,1)=10 \; \; \pi (3,2)=11 \; \; \pi (3,3)=12 \; \; \pi (2,3) =13 \; \; \pi (1,3) =14 \; \; \pi (0,3)=15 $
$\text{etc.} \qquad \pi\text{(Figure 1)}$

Answer 5

WLOG, we are looking for a mapping $\pi \colon \mathbb N^* \times \mathbb N^* \to \mathbb N^*$, where $\mathbb N^*$ denotes the set of positive integers.

This idea is simple and has a geometric/visual appeal to it. You have an infinite grid, but when you look at the finite $n \times n$ initial square segments, you reason that that for starters, you always want to map coordinate pairs from the product diagonal as follows:

$\quad \pi(d,d) = d^2$

Now you have to 'back fill', so that $\pi$ maps these $d \times d$ squares bijectively onto the integer interval $[1,d^2]$.

Now intuitively, you might think that if you are 'close' to the main diagonal, you can start by squaring the larger coordinate and then finding a 'mild' adjustment. The adjustments get more 'heavy handed' as you move away from the diagonal.

Here is the mapping:

$$ \pi(m,n) = \left\{\begin{array}{lr} m^2-2(m-n) , & \text{for } m \ge n\\ n^2-2(n-m)+ 1, & \text{for } m \lt n \end{array}\right\} $$

So,
$\quad \pi(5,3) = 25 - 4 = 21$
$\quad \pi(1,6) = 36 - 10 + 1 = 27$

I used google sheets to verify; here is the visual:

Using induction on the $n \times n$ squares, you can wrap this up.

Exercise: Show that $\pi$ is bijective.

Note: The google sheet/image is off in the $(m,n) = (5,4)$ cell; the correct entry is $\pi(5,4) = 23$.

Answer 6

I want to give one final answer here. It uses the same [$1+2+3+\dots+n$]-math as the Cantor Pairing Function, and also the fact that there is a modulo-3 partition on the integers.

Set

$\qquad \mu (m,n) = \frac{(m-1)(m)}{2} + n + 1$

The mapping $\pi: \mathbb N \times \mathbb N \to \mathbb N$ is defined by

$$ \pi(m,n) = \left\{\begin{array}{lr} 3 \, \mu(m,n) - 2, & \text{for } m \gt n\\ 3m, & \text{for } m = n\\ 3 \, \mu(n,m) - 1,, & \text{for } m \lt n \end{array}\right\} $$

It is easy to show that the function $\pi$ takes the $m \gt n$ ordered pairs bijectively onto $3 {\mathbb N}^{*} -2$. Once you prove that, a $\text{symmetry & translation}$ argument shows that $\pi$ takes the $n \gt m$ ordered pairs bijectively onto $3 \, {\mathbb N}^{*} - 1$. The only thing left is $3 {\mathbb N}$, and that is what the dividing line, the diagonal $m = n$, is used for.

---

This is a 'hack approach' and might have been found before the Cantor Pairing Function was discover in $1878$. In any case, Cantor must have been amazed with his discovery. Several of the other answers shown here split up the domain for the formula definition - they can't outdo Cantor's closed formula.

If you want to find simple solutions, you are hereby warned not to look at the Fueter–Pólya theorem/conjecture wikipedia article.