Visible Portion of the Earth's Surface

Question

EDIT: I need help converting the right side to a function of h

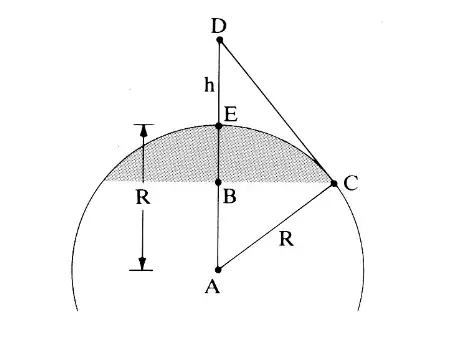
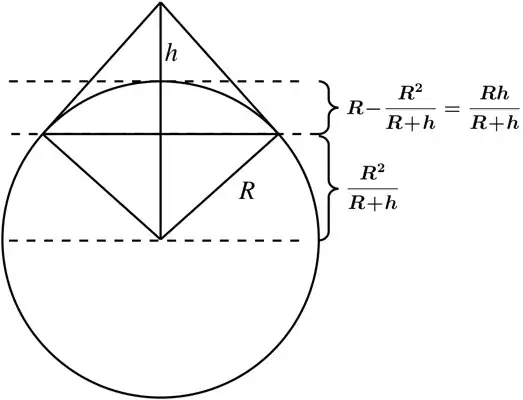
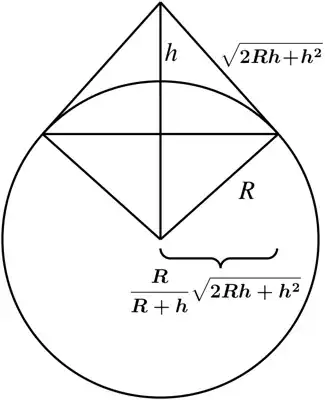
Let $A_h$ be the area of the zone corresponding to height h. If we set up a rectangular co-ordinate syustem with the origin at the center A of the spherical Earth with radius R, and if the surface of the earth is obtained by rotating the curve $x = g(y), y_B \le y \le y_E$ about the y-axis, then the surface area is given by $$A_h = 2\pi \int_{yb}^{ye} g(y) \sqrt{1+[g'(y)]^2} dy$$ 1. Derive a formula for the observable area $A_h$ as a function of the altitude h above the Earth's surface.

Okay, so I've been looking at this problem for a few days now and I'm having trouble deriving this equation based on the pictue. I know I need to revolve the curve $CE$ around the y axis but I'm having a hard time figuring out what the equation will be. I know this has to do with horizon and such, and the equation for line $$CD = \sqrt{h(2R+h)}$$ I also know the $$\sqrt{1+[g'(y)]^2}$$is an arclength

I'm just very confused becuase I know once I plug all these numbers in I will get a constant and integrating a constant is just adding (in this case) a y the result and then plugging in the bounds. Once I find this equation I have the answer for the rest of these problems.

(First post, I'm sorry if this isn't super clear, all help is greatly appreciated)

Answer 1

Geometric Approach

In this answer, it is shown that the area of the green strip on the sphere is the same as the area of the red projection onto the cylinder circumscribing the sphere and sharing its axis with the green strip.

We can compute the height of the cap using similar triangles:

Thus, the area of the cap is $$ 2\pi R\frac{Rh}{R+h}=\frac{2\pi R^2h}{R+h} $$

---

Calculus Approach

Because $\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac xy$, we have

$$ \begin{align} \int_0^{\frac{R}{R+h}\sqrt{2Rh+h^2}}2\pi x\sqrt{1+x^2/y^2}\,\mathrm{d}x &=\int_0^{\frac{R}{R+h}\sqrt{2Rh+h^2}}2\pi R \frac{x}{\sqrt{R^2-x^2}}\,\mathrm{d}x\\ &=-2\pi R\left[\sqrt{R^2-x^2}\right]_0^{\frac{R}{R+h}\sqrt{2Rh+h^2}}\\[6pt] &=\frac{2\pi R^2h}{R+h} \end{align} $$

Answer 2

Adding up the sections of $A_h$ is a lot like stacking up incrementally smaller onion rings and adding up the surface areas of their exteriors.

^{a very dextrous sketch of a stack of onion rings in the shape of the Earth’s crust}

We get the surface area of an onion ring by taking the length of its slant $\ell$ and multiplying it by $2\pi r$, just as if we ‘unwound’ it and calculated the area of the resultant rectangle.

You were right to recognize the arc length formula—that’s exactly what $\ell$ is: a length of arc parametrized by $x$ and $y$. We could also see this by breaking up the crust of Earth into teeny-tiny right triangles, where the hypotenuse measures length $d\ell =\sqrt{dx^2+dy^2}$. However, $g(y)$ is the horizontal piece that we will break into tiny increments, not $x$.

Since you already know the variations of the arc length formula, let’s skip right to $$d\ell=\sqrt{1+\left(\frac{dg}{dy}\right)^2}\,dy =\sqrt{1+\left[g’(y)\right]^2}\,dy$$

Next, to get the area of the exterior surface of each ring, multiply by $2\pi r$, just as if we were dealing with a rectangle of height $d\ell$ and length $2\pi r$. The radius of each ring is given by $g(y)$. This gets us to $$dA_h=2\pi\,g(y)\,\sqrt{1+\left[g’(y)\right]^2}\,dy$$

Finally, we’ll want to add this incremental areas up for all the tiny rings between $y_B$ and $y_E$. Luckily, our variable of integration is already $y$!

$$\begin{align} \int dA_h &= \int_{y_B}^{y_E} 2\pi \,g(y)\,\sqrt{1+\left[g’(y)\right]^2}\,dy \\ A_h &= 2\pi\int_{y_B}^{y_E} g(y)\,\sqrt{1+\left[g’(y)\right]^2}\,dy \\ \end{align}$$

Voilà!

Addendum: I would also recommend researching the calculus-based derivation of the formula for the surface area of a circle and/or the formula for the surface area of a cone.

Answer 3

Given that you already know that you can use the formula

$$A_h = 2\pi \int_{y_B}^{y_E} g(y) \sqrt{1+[g'(y)]^2} dy,$$

you need to figure out the following things:

• Exactly what is the formula for $g(y)$ in this particular problem?
• What is the solution of the integral?
• How is the result a function of $h$?

Consider the integral. You know $g(y)$ has to be the particular function that describes the circle in the figure, and that $g'(y)$ is the derivative of that function, which you can determine when you know exactly what $g(y)$ is. So the only variability to the right of the integral sign is the variable $y,$ which will disappear when you have completely solved the indefinite integral and plugged in the bounds of the definite integral.

To the left of the integral sign you have $2\pi,$ which is a constant. The upper bound is $y_E,$ which you should know is the length of the segment $AE,$ in other words, $y_E = R,$ another constant (since we assume the Earth doesn't grow or shrink while we try different values of $h$).

The only thing left on the right-hand side that isn't completely determined is the symbol $y_B,$ which is equal to the length $AB,$ which does vary as $h$ varies. There are a few different ways you can approach this. Trigonometry works if you're comfortable with it. You can also use the fact that $\triangle ABC$ is similar to $\triangle ACD.$ You known the hypotenuse of $\triangle ABC$ and need one of its legs, namely $AB.$ For any given value of $h$ you can find the hypotenuse of $\triangle ABC$ and you know both of its legs.

So you should be able to write $y_B$ as a function of $h,$ $$ y_B = AB = f(h).$$

But you still need to write out the correct formula for $g(y),$ find $g'(y),$ and find the solution of the definite integral $\int_{y_B}^{y_E} g(y) \sqrt{1+[g'(y)]^2} dy$ in order to be able to "solve" $A_h$ as a function of $h.$

So you have some work to do. It won't get done by staring at it.