0

What is the difference between summation and integration. I have heard that summation is nothing but definite integration. But $ \sum_{i=1}^{10}i $ and $ \int_{i=1}^{10}i $ yields very different values.

$ \sum_{i=1}^{10}i = 55 $

but

$ \int_{i=1}^{10}i = 49.5 $

So where's the catch. I have seen a lot of questions regarding this, but couldn't find a practical example.

Vishnu Vivek
  • 1,441
  • 3
    I think it'll be better for you to wait until you get there in your studies as this is stuff that's pretty difficult to explain from scratch without being facing each other and with a blackboard and a chalk. In very short: definite integration, when possible, gives a number by means of repeatedly carrying on infinite sums of certaing things. – DonAntonio Nov 29 '12 at 12:31
  • @DonAntonio I've pretty much done a number of complex calculations in both summation and integration. But didn't think of this until now :) – Vishnu Vivek Nov 29 '12 at 12:36
  • 1
    Perhaps, this question and answers there are related – S.D. Nov 29 '12 at 12:38
  • @S.D. whoa! there's too much information.. it goes way over my head! Thanks anyways! – Vishnu Vivek Nov 29 '12 at 12:47
  • 1
    Here is a related question – Artem Nov 29 '12 at 13:24

3 Answers3

4

Since a picture says more than words ...

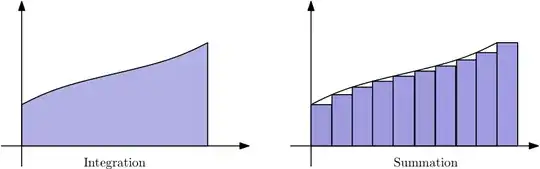
enter image description here

A.Schulz
  • 3,768
  • 3
    In your summation picture, the center of each rectangle should be on the line. This would demonstrate how the summation end up being a higher value than the integration. – woz Nov 29 '12 at 13:53
1

In case $f$ is a simple function such that $f|_{[n,n+1)}$ is constant $f(n)$ for all $n\in\Bbb Z$, then we have $$ \int_0^N f = \sum_{0\le n<N} f(n).$$ In your example the function to integrate was the identity $i\mapsto i$, this is not a simple step function as above, and the integration interval should also be of length $10$ instead of $9$ for a better approximation.

If we choose finer resolutions than $1$, say $\delta$, and suppose now that $f$ is a simple function such that $f|_{[n\delta,(n+1)\delta)}$ is constant for all $n\in\Bbb Z$ then what will we have for $ \displaystyle\int_0^{N\delta} f(x)dx = ?$

And so on, finally every integrable function can be approximated by these kind of simple functions, and as $\delta$ tends to $0$, we'll get the exact integral as limit.

Berci
  • 90,745
1

In simple terms, a summation is the calculation of the sum of discrete values. Consider this example:

$\displaystyle\sum\limits_{i=0}^{10} i = 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55$

Integration is the sum of an infinite number infinitely small values. So, I could not rewite an integration problem as the sum of some numbers, like this:

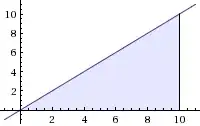
$\int_0^{10} \! x\, \mathrm{d} x, = n + n + ... + n$

Integration is the sum of some numbers, but the $n$ values here cannot be listed because they are infinitely small and non-discrete. It's far more of an abstract concept.

Instead, I think of integration as the area under the graph of the function.

enter image description here

You probably read about Riemann sums, which really highlights the difference between integration and a regular summation.

woz
  • 343
  • thanks.. u mentioned "sum of an infinite number of infinitely small values" within the specified limits. But even then it gives the value of 50, which is less than the actual sum of 55. – Vishnu Vivek Nov 29 '12 at 13:34
  • It's because integration gives an exact calculation of area under the curve, which in this case turns out to be a little less than the very crude estimation you get by doing a summation. The summation is like a Riemann sum with big rectangles instead of infinitely small ones. – woz Nov 29 '12 at 13:49