When does the equation $(A^2+x^2)^sx = C$ have an explicit, closed-form solution?

Question

Solving a certain inverse problem reduces to solving the following elementary equation: $$ (A^2+x^2)^sx = C $$ Here

• $x$ is the unknown. We are interested in $x > 0$.
• $s \in \mathbb{R}$ is a real number.
• $A > 0$ is a fixed real number.
• $C > 0$ is a fixed number, small enough that the equation has at least one solution.

It turns out that depending on the value of $s$ the equation has one or at most two solutions. The left side is strictly increasing when $s \ge -1/2$. It is strictly increasing up to a given point, after which it is strictly decreasing, when $s < -1/2$.

For what values of $s$ does the equation have a closed form solution?

I know of the following cases:

• $s = -1$ second order polynomial
• $s = -1/2$ second order polynomial
• $s = 0$ trivial
• $s = 1/2$ fourth order polynomial with special form
• $s = 1$ third order polynomial, which I did not bother to solve

Are there more, and is it possible to verify that all have been found?

Note that the equation is polynomial if $s$ is rational, but not all polynomial equations have explicit solutions.

Answer 1

Because, in the general case, the equation is a polynomial equation in dependence of algebraically independent monomials ($x,(A^2+x^2)^s)$, the equation cannot be solved for $x$ by rearranging it by applying only finite numbers of elementary functions/operations we can read from the equation.

Other tricks, Special functions, numerical or series solutions could help.
$\ $

$$(A^2+x^2)^sx=C$$

For rational $s$, your equation is an algebraic irrational equation or an algebraic equation over the reals and we can use the known solution formulas and methods for such kinds of equations, e.g. for radicals (radical expressions) as solutions.
see e.g. closed-form expression for roots of a polynomial and related posts

for $(A,C,s,x\in\mathbb{R})\land(A,C,x>0)\land(s\neq 0)$:

$$A^2x^\frac{1}{s}+x^{\frac{1}{s}+2}=C^\frac{1}{s}$$

For rational $s\neq 0$, this equation is related to a trinomial equation and we can use the methods for such kinds of equations.
For real $s\neq 0$, the equation is in a form similar to a trinomial equation. A closed-form solution can be obtained using confluent Fox-Wright Function $\ _1\Psi_1$ therefore.

Szabó, P. G.: On the roots of the trinomial equation. Centr. Eur. J. Operat. Res. 18 (2010) (1) 97-104

Belkić, D.: All the trinomial roots, their powers and logarithms from the Lambert series, Bell polynomials and Fox–Wright function: illustration for genome multiplicity in survival of irradiated cells. J. Math. Chem. 57 (2019) 59-106

Answer 2

In the last two years I have been working with a multi-valued function, which is a modification of Lambert function, $W_q(z)$, https://doi.org/10.1016/j.physa.2019.03.046.

In the original problem, R. V. Ramos propose $W_q(z)$ as solution of the problem $$ W_q(z) \cdot \bigg( 1 + (1-q)\cdot W_q(z) \bigg)^\frac{1}{1-q} = z$$

Actually, we have been using Lambert-Tsallis function in many fields, being able to discuss closed-formula of transcendental equations, writing then in terms of $W_q$.

I have been working a bit to find your answers and make me be understood. For this reason, I decide to change usual notation. Instead of use $W_q(z)$ I will use $W_r(z)$ which is the solution of $$ W_r(z) \cdot \bigg( 1 + \frac{W_r(z)}{r} \bigg)^r = z$$ where $r=1/(q-1)$. From now on I will refer to subindex "r" always.

After a few manipulations and taking in account very relevant aspects ($A,C >0, x> 0, s \in R$), one can show that

$$ x=\sqrt{\frac{A^2}{2s} \cdot W_{2s}\bigg(2s\cdot \big(\frac{C}{A^{2s+1}}\big)^2 \bigg) } \ \ \ \ \ (1)$$

As previously said, $W_r(z)$ is a multivalued function. In this way, you have to test which of the solutions found will be a truly solution of your original problem. But let's go to the considerations

$$ x>0 \implies \bigg \{ \begin{matrix} s,W_{2s} > 0 \ \ \ \ \ (2.1) \\ s,W_{2s} < 0 \ \ \ \ \ (2.2) \end{matrix} $$

About $2.1$

In $W_r(z)$ when $r,z >0$ at least one solution will be positive. No matter if $r>0$ is integer or not. In your case, $z>0$ when $s>0$. Following, you have some results using Eq (1). Only those in bold are accepted answers and they are presented with 5 decimal points.

\begin{matrix} s & A & C & r & z & W & x \\ \textbf{+0.2500} & \textbf{+4.0000} & \textbf{+3.1416} & \textbf{+0.5000} & \textbf{+0.0771} & \textbf{(+0.07209 , +0.00000i)} & \textbf{(+1.51879 , +0.00000i)} \\ +0.5000 & +4.0000 & +3.1416 & +1.0000 & +0.0386 & (-1.03717 , +0.00000i) & (+0.00000 , +4.07366i) \\ \textbf{+0.5000} & \textbf{+4.0000} & \textbf{+3.1416} & \textbf{+1.0000} & \textbf{+0.0386} & \textbf{(+0.03717 , +0.00000i)} & \textbf{(+0.77119 , +0.00001i)} \\ +1.0000 & +4.0000 & +3.1416 & +2.0000 & +0.0048 & (-2.00240 , +0.09803i) & (+0.09794 , +4.00360i) \\ +1.0000 & +4.0000 & +3.1416 & +2.0000 & +0.0048 & (-2.00240 , -0.09803i) & (+0.09794 , -4.00359i) \\ \textbf{+1.0000} & \textbf{+4.0000} & \textbf{+3.1416} & \textbf{+2.0000} & \textbf{+0.0048} & \textbf{(+0.00480 , -0.00000i)} & \textbf{(+0.19588 , -0.00002i)} \\ +3.0000 & +4.0000 & +3.1416 & +6.0000 & +0.0000 & (-6.29798 , -0.17025i) & (+0.05539 , -4.09850i) \\ +3.0000 & +4.0000 & +3.1416 & +6.0000 & +0.0000 & (-6.29798 , +0.17025i) & (+0.05539 , +4.09850i) \\ +3.0000 & +4.0000 & +3.1416 & +6.0000 & +0.0000 & (-6.00332 , -0.34584i) & (+0.11520 , -4.00276i) \\ +3.0000 & +4.0000 & +3.1416 & +6.0000 & +0.0000 & (-6.00332 , +0.34584i) & (+0.11520 , +4.00276i) \\ +3.0000 & +4.0000 & +3.1416 & +6.0000 & +0.0000 & (-5.69871 , +0.17602i) & (+0.06020 , +3.89874i) \\ +3.0000 & +4.0000 & +3.1416 & +6.0000 & +0.0000 & (-5.69871 , -0.17602i) & (+0.06020 , -3.89874i) \\ \textbf{+3.0000} & \textbf{+4.0000} & \textbf{+3.1416} & \textbf{+6.0000} & \textbf{+0.0000} & \textbf{(+0.00000 , +0.00000i)} & \textbf{(+0.00077 , +0.00000i)} \\ +3.0000 & +3.1416 & +4.0000 & +6.0000 & +0.0000 & (-6.56464 , -0.31991i) & (+0.08005 , -3.28707i) \\ +3.0000 & +3.1416 & +4.0000 & +6.0000 & +0.0000 & (-6.56464 , +0.31991i) & (+0.08005 , +3.28707i) \\ +3.0000 & +3.1416 & +4.0000 & +6.0000 & +0.0000 & (-6.01195 , +0.65792i) & (+0.17182 , +3.14941i) \\ +3.0000 & +3.1416 & +4.0000 & +6.0000 & +0.0000 & (-6.01195 , -0.65792i) & (+0.17182 , -3.14941i) \\ +3.0000 & +3.1416 & +4.0000 & +6.0000 & +0.0000 & (-5.42341 , -0.34099i) & (+0.09385 , -2.98830i) \\ +3.0000 & +3.1416 & +4.0000 & +6.0000 & +0.0000 & (-5.42341 , +0.34099i) & (+0.09385 , +2.98830i) \\ \textbf{+3.0000} & \textbf{+3.1416} & \textbf{+4.0000} & \textbf{+6.0000} & \textbf{+0.0000} & \textbf{(+0.00001 , +0.00000i)} & \textbf{(+0.00416 , +0.00000i)} \\ \end{matrix}

About $2.2$

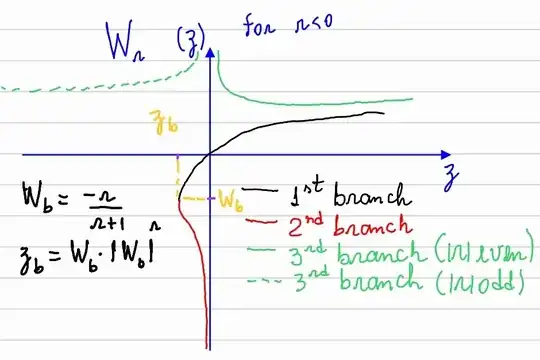
There is a second possibilty to exist $x>0$. If $s<0$ we have $r<0$ and if $W_r(z)<0$ it could have at least one possible solution $x>0$. The figure below illustrates behavior of Lambert-Tsallis function when $r \in Z_{-}^{*} < -1$.

$r \in Z_{-}^{*} $" />

The case $\mathbf{ r < -1}$ or $\mathbf{s < -1/2}$

If we look to such a figure, when the condition $z_b < z < 0$ is satisfied there are 2 possible $W_r(z) <0$ that could generate solutions for $x$ that can be written as

$$ z_b < \frac{r\cdot C^2}{A^{2r+2}} <0 $$ $$ \implies C< C_{Thr}= A^{r+1}\cdot \sqrt{-\frac{1}{r+1} \cdot (\frac{r}{r+1})^r} $$

When $s<-1/2$, you see that there is a relationship that must be satisfied if you want to have $x>0$. Let's see somes examples.

\begin{matrix} A & s & C_{Thr} & C/C_{Thr} & r & z & W & x\\ \textbf{+3.1416} & \textbf{-1/1.99} & \textbf{+0.9787} & \textbf{+0.9000} & \textbf{-1.0050} & \textbf{-0.7887} & \textbf{(-3.80307 , -0.00000i)} & \textbf{(+6.11123 , +0.00000i)} \\ \textbf{+3.1416} & \textbf{-1/1.9} & \textbf{+0.8481} & \textbf{+0.9000} & \textbf{-1.0526} & \textbf{-0.6918} & \textbf{(-2.45948 , +0.00000i)} & \textbf{(+4.80212 , -0.00000i)} \\ \textbf{+3.1416} & \textbf{-2/3} & \textbf{+0.4693} & \textbf{+0.9000} & \textbf{-1.3333} & \textbf{-0.5103} & \textbf{(-1.20217 , +0.00000i)} & \textbf{(+2.98307 , -0.00000i)} \\ \textbf{+3.1416} & \textbf{-1.0000} & \textbf{+0.1592} & \textbf{+0.9000} & \textbf{-2.0000} & \textbf{-0.4050} & \textbf{(-5.09081 , +0.00000i)} & \textbf{(+5.01220 , -0.00000i)} \\ \textbf{+3.1416} & \textbf{-1.0000} & \textbf{+0.1592} & \textbf{+0.9000} & \textbf{-2.0000} & \textbf{-0.4050} & \textbf{(-0.78573 , +0.00000i)} & \textbf{(+1.96912 , -0.00000i)} \\ \textbf{+3.1416} & \textbf{-1.5000} & \textbf{+0.0390} & \textbf{+0.9000} & \textbf{-3.0000} & \textbf{-0.3600} & \textbf{(-3.24070 , +0.00000i)} & \textbf{(+3.26519 , -0.00000i)} \\ \textbf{+3.1416} & \textbf{-1.5000} & \textbf{+0.0390} & \textbf{+0.9000} & \textbf{-3.0000} & \textbf{-0.3600} & \textbf{(-0.64650 , +0.00000i)} & \textbf{(+1.45839 , -0.00000i)} \\ +3.1416 & -1.5000 & +0.0390 & +0.9000 & -3.0000 & -0.3600 & (+12.88720 , +0.00000i) & (+0.00000 , -6.51131i) \\ +3.1416 & -1.5000 & +0.0390 & +1.1000 & -3.0000 & -0.5378 & (-1.13571 , +1.05148i) & (+2.10097 , -0.82325i) \\ +3.1416 & -1.5000 & +0.0390 & +1.1000 & -3.0000 & -0.5378 & (-1.13571 , -1.05148i) & (+2.10097 , +0.82325i) \\ +3.1416 & -1.5000 & +0.0390 & +1.1000 & -3.0000 & -0.5378 & (+11.27141 , -0.00000i) & (+0.00000 , +6.08946i) \\ \textbf{+3.1416} & \textbf{-2.0000} & \textbf{+0.0105} & \textbf{+0.9000} & \textbf{-4.0000} & \textbf{-0.3417} & \textbf{(-2.71659 , -0.00000i)} & \textbf{(+2.58900 , +0.00000i)} \\ \textbf{+3.1416} & \textbf{-2.0000} & \textbf{+0.0105} & \textbf{+0.9000} & \textbf{-4.0000} & \textbf{-0.3417} & \textbf{(-0.59515 , -0.00000i)} & \textbf{(+1.21181 , +0.00000i)} \\ +3.1416 & -2.0000 & +0.0105 & +0.9000 & -4.0000 & -0.3417 & (+9.65587 , +8.06864i) & (+1.90040 , -5.23798i) \\ +3.1416 & -2.0000 & +0.0105 & +0.9000 & -4.0000 & -0.3417 & (+9.65587 , -8.06864i) & (+1.90040 , +5.23798i) \\ +3.1416 & -2.0000 & +0.0105 & +1.0100 & -4.0000 & -0.4304 & (-1.30394 , +0.30543i) & (+1.80579 , -0.20867i) \\ +3.1416 & -2.0000 & +0.0105 & +1.0100 & -4.0000 & -0.4304 & (-1.30394 , -0.30543i) & (+1.80579 , +0.20867i) \\ +3.1416 & -2.0000 & +0.0105 & +1.0100 & -4.0000 & -0.4304 & (+9.30394 , -7.49468i) & (+1.80579 , +5.12030i) \\ +3.1416 & -2.0000 & +0.0105 & +1.0100 & -4.0000 & -0.4304 & (+9.30394 , +7.49468i) & (+1.80579 , -5.12030i) \\ \end{matrix}

The case $\mathbf{ r = -1}$ or $\mathbf{s = -1/2}$

In the end of your question, you have mentioned that $s=-1/2$ results like an inflection point. Actually, this is an special case $W_r(z)$ function.

$$W_{-1}(z)=\frac{z}{z+1}$$

There is no branch point, like Lambert Function. In this case, you can see the solution $$ x = \frac{A \cdot C}{\sqrt{1-C^2}}$$

But there is a point that cause problem. It corresponds to $z=-1$ or $C= A^{2r+1}=1 $.

The case $\mathbf{ -1 < r < 0}$ or $\mathbf{-1/2 < s < 0}$

In that region, there is no branch point also. Actually if you try to apply the formula for $C_{Threshold}$ you will note that I would correspond to $C \notin R$. It says for us there is no branch point.

The solution found in this region will be positive and it will increase until the limit of $x$ corresponding to $r=1$ but for $C\neq 1$. I would have to analyse the case when $C>1$ but I believe it would generate $x<0$ which is not of your interest. Maybe, because of this you have imposed a condition of C small. Following some examples

\begin{matrix} A & C & s & r & z & x_{analytic} & W & x_{numeric} \\ \textbf{+3.1416} & \textbf{+0.5000} & \textbf{-1/5} & \textbf{-0.4000} & \textbf{-0.0253} & \textbf{+1.8138} & \textbf{(-0.02596 , +0.00000i)} & \textbf{(+0.80037 , -0.00000i)} \\ \textbf{+3.1416} & \textbf{+0.5000} & \textbf{-1/2.5} & \textbf{-0.8000} & \textbf{-0.1265} & \textbf{+1.8138} & \textbf{(-0.14450 , -0.00000i)} & \textbf{(+1.33516 , +0.00000i)} \\ \textbf{+3.1416} & \textbf{+0.5000} & \textbf{-1/2.1} & \textbf{-0.9524} & \textbf{-0.2135} & \textbf{+1.8138} & \textbf{(-0.27100 , -0.00000i)} & \textbf{(+1.67584 , +0.00000i)} \\ \textbf{+3.1416} & \textbf{+0.5000} & \textbf{-1/2.025} & \textbf{-0.9877} & \textbf{-0.2400} & \textbf{+1.8138} & \textbf{(-0.31567 , -0.00000i)} & \textbf{(+1.77608 , +0.00000i)} \\ \textbf{+3.1416} & \textbf{+0.5000} & \textbf{-1/2.00025} & \textbf{-0.9999} & \textbf{-0.2499} & \textbf{+1.8138} & \textbf{(-0.33315 , -0.00000i)} & \textbf{(+1.81341 , +0.00000i)} \\ \textbf{+3.1416} & \textbf{+0.5000} & \textbf{-0.5000} & \textbf{-1.0000} & \textbf{-0.2500} & \textbf{+1.8138} & \textbf{(-0.33333 , +0.00000i)} & \textbf{(+1.81380 , -0.00000i)} \\ \end{matrix}

Answer 3

In general we should not expect a closed-form solution when $s$ is irrational, so suppose that $s = \frac{m}{n}$ for $m \in \Bbb Z$, $n \in \Bbb Z^+$, $\operatorname{gcd}(m, n) = 1$. Rearranging gives $$(A^2 + x^2)^m x^n = D,$$ where $D := C^n$.

If $m \geq 0$ and $n$ is odd, then the equation is polynomial of degree $2 m + n$ in $x$, which is no more than $4$ (guaranteeing the existence of solution in radicals) if $(m, n) \in \{(0, 1), (1, 1)\}$, i.e., if $s = \frac{m}{n} \in \{0, 1\}$.

If $m \geq 0$ and $n$ is even (which means that $m$ is odd), the equation is polynomial of degree $m + \frac{n}{2}$ in $x^2$, so we can find an explicit expression for $x^2$, hence for $x$, if this degree is no more than $4$, that is, if $(m, n) \in \left\{(1, 2), (1, 4), (3, 2)\right\}$, i.e., if $s = \frac{m}{n} \in \left\{\frac{1}{4}, \frac{1}{2}, \frac{3}{2}\right\}$

If $m < 0$ and $n$ is odd, then multiplying both sides by $(A^2 + x^2)^{|m|}$ leaves the polynomial equation $$x^n = D (A^2 + x^2)^{|m|} ,$$ which has degree $\operatorname{max}(2|m|, n)$, which in turn is $\leq 4$ iff $|m| \in \{1, 2\}$ and $n \in \{1, 3\}$, i.e., iff $s = \frac{m}{n} \in \left\{-2, -1, -\frac{2}{3}, -\frac{1}{3}\right\}$.

Finally, if $m < 0$ and $n$ is even (so that again $m$ is odd), then the rearranged equation is polynomial of degree $\operatorname{max}\left(|m|, \frac{n}{2}\right)$ in $x^2$, so $|m| \in \{1, 3\}$ and $n \in \{2, 4, 6, 8\}$, hence $s \in \left\{-\frac{3}{2}, -\frac{3}{4}, -\frac{1}{2}, -\frac{3}{8}, -\frac{1}{4}, -\frac{1}{6}, -\frac{1}{8} \right\}$.

Collating the above results, there are closed-form solutions (at least) when $$s \in \left\{-2, -\frac{3}{2}, -1, -\frac{3}{4}, -\frac{2}{3}, -\frac{1}{2}, -\frac{3}{8}, -\frac{1}{3}, -\frac{1}{4}, -\frac{1}{6}, -\frac{1}{8}, 0, \frac{1}{4}, \frac{1}{2}, 1, \frac{3}{2}\right\}.$$