Graphs that "polygonize" a manifold

Question

It's rather easy to conceptualize a covering of the Euclidean plane by a countable set of convex but otherwise arbitrarily sized and shaped polygons (seen as subsets of the plane) without overlaps. It can - without loss of generality? - be required that two such polygons do share exactly one complete edge or none.

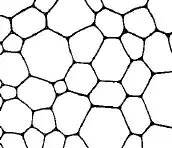
Is there an official name of such a covering?

I guess "polygonization of the plane" is not utterly wrong, but misses some aspects: convexity and uniqueness of shared edges.

Anyway: a polygonization of the plane induces an (infinite) graph with obvious vertices and edges.

(How) can such a graph be characterized?
("A graph is induced by a polygonization of the plane iff it is planar, 2-edge-connected, and ...")

The Euclidean plane is not the only manifold that can be polygonized in the way described above: there are polygonizations of the sphere, the torus and so on and so on.

(How) can the graphs be characterized, that polygonize any manifold?

Answer 1

I could be wrong but what the concept you are looking for looks pretty much like a Voronoi diagram.

An excerpt form Wikipedia:

In mathematics, a Voronoi diagram is a partitioning of a plane into regions based on distance to points in a specific subset of the plane. That set of points (called seeds, sites, or generators) is specified beforehand, and for each seed there is a corresponding region consisting of all points closer to that seed than to any other. These regions are called Voronoi cells. The Voronoi diagram of a set of points is dual to its Delaunay triangulation.

And this is how it looks like (credits to Wikipedia):

There is a quite easy to follow algorithm to generate a Voronoi diagram of a given space. Basically you will require a "seed" of points to make the partitions. They can be random, so the cells will be random every time you apply the procedure from scratch.

Some time ago I was also trying to understand how it is applied, here is a Voronoi diagram of a Sierpinski attractor.