Let $p_i$ denote the $i^{\rm th}$ prime number, and let $\lfloor x \rfloor$ denote the greatest integer smaller than or equal to $x$. Then does the sum defined by:
$$ \sum_{n=0}^{\infty} \frac{1}{p_{\lfloor\pi n\rfloor}} $$
converge?
Computing the partial sum up to $n=3\times10^7$ yields a value of about $\approx 0.890694\ldots$, and Wolfram Alpha gives the following plot, suggesting that the sum might be convergent:
Note that Wolfram does not explicitly state that the sum is non-convergent, as it does for instance in the case $\sum_{n=0}^{\infty} \frac{1}{p_{2n}}$.
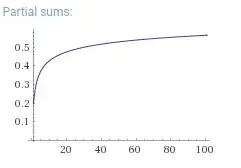
sum 1/Prime[floor(pi*n)], for n=1 to infinityinto https://www.wolframalpha.com – Klangen Oct 12 '17 at 10:39https://www.wolframalpha.com/input/?i=sum+1%2FPrime%5B2*n%5D,+for+n%3D1+to+infinity– Klangen Oct 12 '17 at 10:56