absolute value of 2 complex exponentials

Question

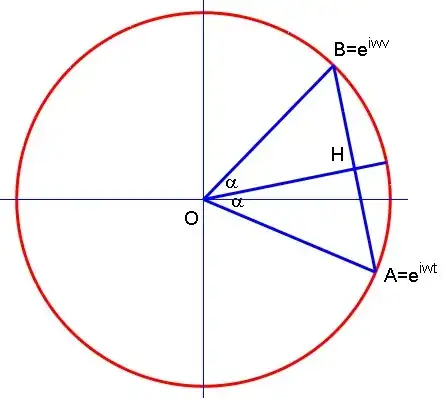
Sorry if this is a dumb question. Trying to understand what this simplifies to:

$$f(t) = |e^{iwt} - e^{iwv}|$$

I don't understand how to get a nice numerical answer to this as the exponentials use different variables to one another...

Its related to the proof of the Fourier Condition of Lipschitz regularity in Stephane Mallat's "Wavelet tour of signal processing book". (Theorem 6.1, page 165)

Many thanks for any answers!

EDIT: Looking at folks answers it seems pretty clear to me you can get a few different solutions to this...for extra clarification, the "solution" in Mallat's book is:

For (condition 1) $$\frac{1}{|t - v|}<= |w|$$ $$\frac{|exp(iwt) - exp(iwv)|}{|t - v|^\alpha} <= \frac{2}{|t - v|^\alpha} <= 2|w|^\alpha$$

For (condition 2) $$\frac{1}{|t - v|}>= |w|$$

$$\frac{|exp(iwt) - exp(iwv)|}{|t - v|^\alpha} <= \frac{|w||t - v|}{|t - v|^\alpha} <= |w|^\alpha$$

So far only one person has given a solution to the problem at the top which could give the solution for condition 1...I still have no idea how Mallat's achieved it for condition 2!

Answer 1

We have that

$$|e^{i\omega t} - e^{i\omega v}|\le |e^{i\omega t}|+| e^{i\omega v}|\le 1+1=2.$$

To get a better bound we note that (assume $\omega>0,$ $t<v$, without lost of generality)

$$|e^{i\omega t} - e^{i\omega v}| = \left|\int_{\omega t}^{\omega v} ie^{it}\,dt\right|\le \int_{\omega t}^{\omega v} |ie^{it}|\,dt = \omega(v-t).$$

Answer 2

I am not sure you will find this as a simplification but we can obtain a nice upper bound in the case that $w,v,t \in \mathbb{R}$

We have

$$\exp(iwt)=cis(wt)\\\exp(iwv)=cis(vt)$$

So $$f(t)=|cis(wt)-cis(vt)|\le|wt-wv|\le|w||t-v|$$

The inequality holds for $w,v,t \in \mathbb{R}$

Answer 3

You can pull a factor out,

$$|e^{iwt}-e^{iwu}|=|e^{iwt}||1-e^{iw(u-t)}|=|1-e^{iw(u-t)}|.$$

Then

$$\sqrt{(1-\cos \theta)^2+(\sin \theta)^2}=\sqrt{2-2\cos \theta)}=\sqrt{4\sin^2\frac{\theta}2}=\left|2\sin\frac{\theta}2\right|\le\theta.$$

Answer 4

(see figure below)

$$\tag{1} |exp(iwt) - exp(iwv)|=2 \left|\sin \left( \dfrac{w(v-t)}{2} \right)\right|$$

on a geometrical basis that can be explained in this way :

Let $A=(cos(wt),sin(wt))$ and $B=(cos(wv),sin(wv))$.

Thus angle $AOB=|wv-wt|=|w(v-t)|$. Let us denote this angle by $2\alpha$.

Thus, we have $\alpha = \dfrac{|w(v-t)|}{2}.$

We have to express $AB=2OH$ where $H$ is the midpoint of $AB$.

The essential point is that $AOB$ is an isosceles triangle ; consequences:

• $AH$ is orthogonal to $AB$ and

• angle $\alpha$ = angle $HOA$ = angle $HOB = w|t-v|/2. $

Thus $AH = \sin(\alpha)$ ; then $AB=2AH=2\sin(\alpha)$ yielding relationship (1).

Remark: As a consequence of (1), this expression is bounded by

$$ 2 \left| \dfrac{w(v-t)}{2} \right| =\left| w(v-t) \right|$$