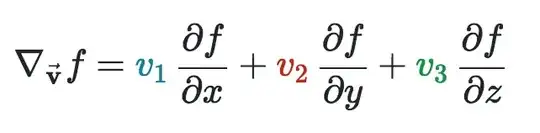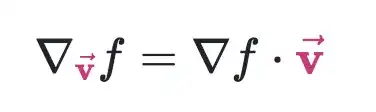3

I'm learning Directional Derivative on Khan Academy. Here is the definition of Directional Derivative:

enter image description here

So the formula for calculating directional derivative is:

enter image description here

But as I knew, the dot product should be:

enter image description here

I don't understand this point. Please explain for me why the formula for calculating directional derivative doesn't have "cos($\alpha$)".

ned grekerzberg
  • 977
hqt
  • 759
  • 4
  • 9
  • 19
  • That’s not the only way to define the dot product. – amd Oct 10 '17 at 08:50
  • so you means we have 2 ways for calculating dot product. And as I guess, by using those 2 ways, I can calculate cos(alpha) between those 2 vectors. For example, vector (a1,b1) and vector (a2,b2). cos(alpha) = (a1a2+ b1b2) / (square_root(a1^2+b1^2) * square_root(a2^2+b2^2)) – hqt Oct 10 '17 at 08:58
  • 1
    The dot product should be $$a \cdot b$$ –  Oct 10 '17 at 09:23
  • @hqt Just so. This works in higher-dimensional spaces, too. In fact, you can take that equivalence as the definition of angle in any vector space equipped with an inner product. – amd Oct 10 '17 at 20:40

1 Answers1

1

The Dot Product of two vectors $x=[x_1,x_2\cdots, x_n], a=[a_1,a_2\cdots, a_n]$ is algebraically defined as $$x\cdot a=\sum_{i=1}^nx_ia_i=x_1a_1+x_2a_2+\cdots+x_na_n$$ In your case we have the vectors $v=[v_1, v_2, v_3]$ and $df=\Large [\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y},\frac{\partial f}{\partial z}]$.

I hope it is clear now why the formula described is correct.


In the Euclidean $2D$-space indeed we do have an equivalent geometric form involving $\cos$ as you mention in your question.

MathematicianByMistake
  • 5,495
  • so cos(alpha) version only appeared in Euclidean 2-D space? I asked this because there is a proof why "gradient descent of multivariable function is a steepest ascent" using this formula for prof. – hqt Oct 10 '17 at 15:26
  • For example here: https://math.stackexchange.com/questions/223252/why-is-gradient-the-direction-of-steepest-ascent – hqt Oct 10 '17 at 15:27
  • 1
    The “geometric form” is valid in a Euclidean space of any dimension. Indeed, it can be taken as the definition of the angle between two vectors in an inner product space. – amd Oct 10 '17 at 17:35
  • @amd Thank you for the clarifications. I did not mean to imply that the geometric form is somehow restricted to $2D$ space but I see that my wording was less than perfect.. – MathematicianByMistake Oct 10 '17 at 21:46