3

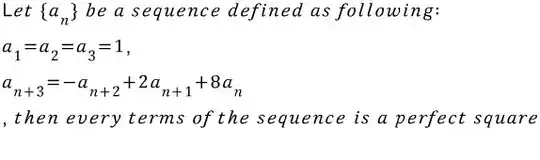
enter image description here

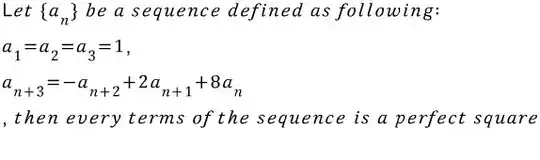
enter image description here

I would be happy if you let me know how to tackle this problem. Thanks.

Walt van Amstel
  • 925
user488002
  • 91
  • 3
    What have you tried? How familiar are you with the theory of linear recurrence relations? – Carl Schildkraut Oct 05 '17 at 15:49
  • 1
    I've googled about this problem and reached https://math.stackexchange.com/questions/1869842/prove-that-a-n-is-a-perfect-square https://math.stackexchange.com/questions/1901245/how-to-prove-each-element-of-the-following-sequence-is-a-perfect-square, and https://math.stackexchange.com/questions/1202991/proving-an-expression-is-perfect-square. I'm trying to apply those techniques. – user488002 Oct 05 '17 at 15:54

2 Answers2

4

Hint: You're on the right track. There does exist a linear recurrence relation for a sequence defined by some square roots of $a_n$, but not necessarily the positive ones (e.g. instead of $b_6=5$, you might have $b_6=-5$). Can you try to find a recurrence relation from there?

Carl Schildkraut
  • 32,931
  • Well.. I tried bn+3 = xbn+2 + ybn+1 + zbn + w, which yields x=-1, y=1, z=4, w=-1 for n=1,2,3,4, but it does not work for n=5, 6,... . I guess I should pick "correct sign" of numbers(positive or negative). Need an additional help. – user488002 Oct 06 '17 at 04:28
  • oh I got it. Define a sequence {bn} as b1=1, b2=-1, and bn+2 = -bn+1 - 2bn, then an = (bn)^2 by induction! – user488002 Oct 06 '17 at 12:21
  • @user488002 Yep! – Carl Schildkraut Oct 06 '17 at 13:50
2

The idea is to look for a linear recurrence relation among the square roots. Say we have a relation $b_n=c_1b_{n-1}+c_2b_{n-2}$. Assuming the roots of the characteristic polynomial are distinct, the general formula should be $b_n=d_1\lambda_1^n+d_2\lambda_2^n$ where $d_1,d_2$ are constants and $\lambda_1,\lambda_2$ are the roots of the characteristic polynomial. Then $b_n^2=d_1^2\left(\lambda_1^2\right)^n+d_2^2\left(\lambda_2^2\right)^n+2d_1d_2\left(\lambda_1\lambda_2\right)^n$, so it has a recurrence relation of order 3 where the product of two of the roots of the characteristic polynomial is the square of the third.

Now observe that 2 is a root of the characteristic polynomial (and you should observe this, because one thing to do when looking for the roots of a polynomial is apply the rational root theorem to look for rational roots). Also, the product of the other two roots is 4, which is $2^2$. This suggests that the square roots should satisfy a reucurrence relation with characteristic polynomial $\frac{x^3+x^2-2x-8}{x-2}$; this gives you the recurrence to test and it works, once you try sufficiently many combinations of positive and negative signs on the first two terms of the recurrence.

alphacapture
  • 2,981