3

I didn't undestand how this values, that are values in galois field $GF(2^{3})$. in thes below tables are obtained. Someone could explain me?

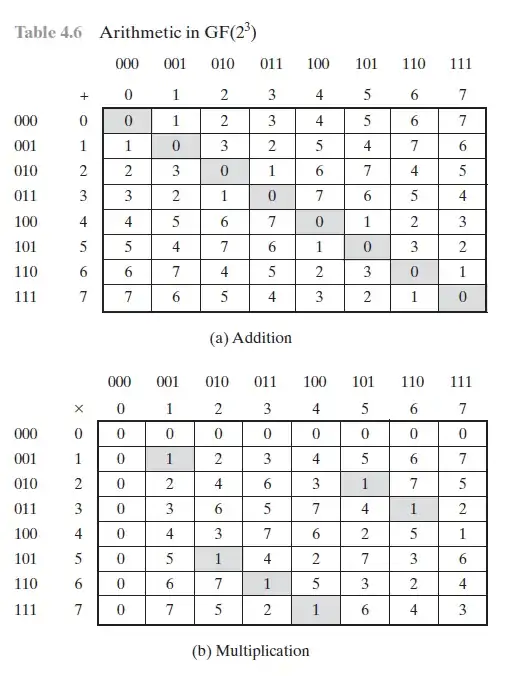
enter image description here

hmakholm left over Monica
  • 286,031
Mazzy
  • 281
  • 1
    The answers below are very good. If they do not fit your background, you can also try the second half (you need to scroll down a bit) of my answer to a coding theoretical question. There I explicitly construct the field $GF(8)$, and show how to do field addition and multiplication there. That should also help you in reproducing these tables. – Jyrki Lahtonen Nov 28 '12 at 13:33

2 Answers2

4

The field is represented as a field of polynomials of degree $\leq2$ over the field $\mathbb F_2=\{0,1\}$. The notation $(cba)$ means $cX^2 + bX+a$. Since $1+1=0$ the addition table is clear, e.g. $(011)+(010)=(001)$.

For the multiplication, we need to find out what should $X^3$ be rewritten to. From the multiplication table you see that $X^3=X^2 \cdot X^1=(100)\cdot(010)=(011)$ and hence $X^3=X^1+1$ and therefore $X^4=X^2+X$. Now, you can multiply any two polynomials $(cba)\cdot(CBA)$ and rewrite them with degree $\leq2$.

Example: $$(111)\cdot(101)=(X^2+X+1)(X^2+1)=X^4+X^3+2X^2+X+1=X^4+X^3+0+X+1= (X^2+X)+(X+1)+X+1=X^2+X=(110).$$

In general, to find a representation of $\mathbb{GF}(p^n)$ you have to find a polynomial $f(X)$ of degree $n$ that is irreducible over $\mathbb F_p$. Irreducible means that if $f=gh$ for polynomials $g,h$, then either $g(X)=1$ or $h(X)=1$. Then you have that $\mathbb{GF}(p^n)\simeq \mathbb F[X]/f$.

yo'
  • 4,506
  • you say that $1+1=0$. In binary $1+1=10$ but in this example why $1+1=0$ ? – Mazzy Nov 27 '12 at 12:38
  • 2
    Because we treat is as polynomials over a field $\mathbb F_2$ with operations modulo $2$, not as numbers. So e.g. $(001)+(001)=1+1=2=0$ or $(010)+(010)=X+X=2X=0$. – yo' Nov 27 '12 at 13:29
  • 1
    ok I understood – Mazzy Nov 27 '12 at 13:30
3

Evidently, each element of the field is being represented in two different ways, as a string of $3$ bits, and as a number between $0$ and $7$, inclusive. The translation between the two representations is just that the $3$-bit string $abc$ corresponds to the number $4a+2b+c$; that is, we're just doing binary numbers here.

The addition is best understood by treating the $3$-bit strings as objects to be added without carry from one bit to the next. To put it another way, think of $abc$ as standing for the ordered triple $(a,b,c)$ and doing addition modulo $2$.

The multiplication is best understood by interpreting the $3$-bit string $abc$ as the polynomial $ax^2+bx+c$ and then doing multiplication modulo $2$ on the coefficients but also modulo $x^3+x+1$. That is, any time you get a power of $x$ higher than the second, you replace $x^3$ with $x+1$, and $x^4$ with $x^2+x$. Try it, you'll see how it works.

Gerry Myerson
  • 179,216