1

On an infinite frying pan, there is a bounded pancake. Prove that one can make a straight cut in any given direction (that is, parallel to a given line) that splits the pancake in halves of equal area.

I think that you can use intermediate value theorem, but I'm not quite sure where to start or how to apply the theorem

Vinny Chase
  • 1,541

1 Answers1

1

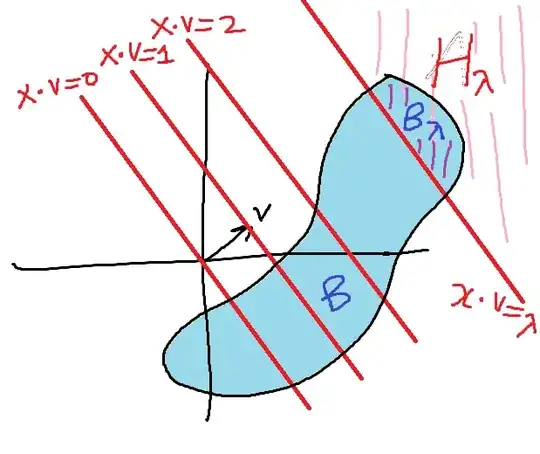
Here's the outline of a solution. For every nonzero vector $v \in \mathbb{R}^n$ and $\lambda \in \mathbb{R}$ consider the half-space defined as $H_{\lambda} = x \cdot v \geq \lambda$. For any bounded region $B$, let $B_{\lambda} = H_{\lambda} \cap B$. This corresponds to the part of $B$ on side of a cut that runs parallel to any vector perpendicular to $v$. Fix the vector $v$ and define the function $f(\lambda) = \mbox{Volume}(B_\lambda)$. Show that $f(\lambda)$ is continuous, that $\lim_{\lambda \to \infty} f(\lambda) = 0$, and that $\lim_{\lambda \to -\infty} f(\lambda) = \mbox{Volume}(B)$. Finally, apply the intermediate value theorem.

Perhaps this picture might help: enter image description here

Elchanan Solomon
  • 30,807
  • A minor nitpick: we are assuming that $B$ is a bounded and measurable set, then exploiting the absolute continuity of the Lebesgue measure (https://math.stackexchange.com/questions/535185/absolute-continuity-of-the-lebesgue-integral). – Jack D'Aurizio Oct 03 '17 at 16:56
  • @ElchananSolomon Could you please explain why those limits turn out the way they do? I don't see why f($\lambda$) would go to 0 as $\lambda$ goes to infinity? Isn't f(\lambda) the volume of B$_{\lambda}$? Why would the volume go to 0? – Vinny Chase Oct 04 '17 at 19:56
  • @JackD'Aurizio We haven't done Lebesque Measure yet. Is there a way to do this without involving that? – Vinny Chase Oct 04 '17 at 19:57
  • @VinnyChase: it depends on your definition of area. What is it? – Jack D'Aurizio Oct 04 '17 at 19:58