1

I have a line that has a series of vertices and segments. From iterating through the vertices, I can calculate the length of the line (approximately) by determine the great circle distance using the Haversine formula.

My next challenge to calculate a point at a given distance. Initial research shows that in a Cartesian space, I can treat the line segment as a vector, and thus normalize it as shown here. However, this doesn't work due to the curvature of the Earth.

So how would one find a point for my scenario? Alter the Haversine to reverse engineer it?

pstatix
  • 239
  • 2
    Most applications of math to real life involve some kind of approximation, if only because our measuring instruments are imperfect. But on a sphere, the haversine formula is an exact solution for the length of a great-circle arc, so what particular reason do you have for saying you only approximately calculate the length of a line by the haversine formula? Is your line curved in a way that great-circle segments cannot follow, are you concerned with distances on a spheroidal model of the Earth, or is there some other source of inexactness you are concerned about in your calculation? – David K Oct 04 '17 at 14:16

1 Answers1

4

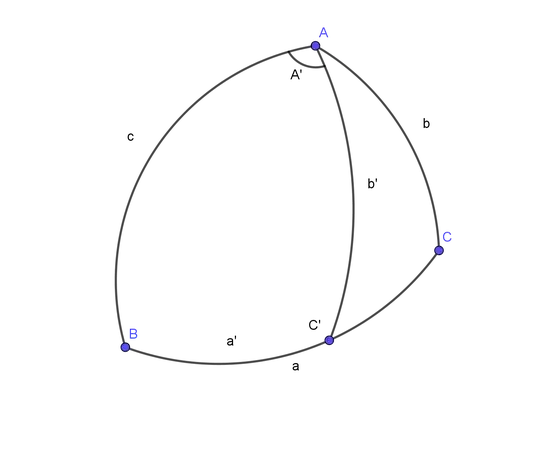
Spherical Trigonometry

We can find the coordinates of an intermediate point through repeated application of the law of cosines of spherical trigonometry: $$\cos a = \cos b \cos c + \sin b \sin c \cos A$$
or equivalently $$\cos A = \frac{\cos a - \cos b \cos c}{\sin b \sin c}$$

In the above figure, A is the north pole, and arc BC is the great circle route from B to C. We are given the spherical coordinates of B and C, and the angle a'. We want to compute the spherical coordinates of point C'.

In spherical trigonometry, a side of a triangle is measured by the angle subtended at the center of the sphere. To convert an angle to a distance on the surface of the earth, which is assumed to be a sphere, we would multiply the angle in radians by the radius of the earth. The convention in spherical trigonometry is that a point is identified by its longitude, $\theta$, and its co-latitude, $\phi$. The co-latitude is zero at the north pole, unlike geographic latitude which is $90$ degrees at the north pole.

Let's say the spherical coordinates of B are $(\theta_1, \phi_1)$, those of C are $(\theta_2, \phi_2)$, and we know the angle a'. We want to compute the spherical coordinates of C, $(\theta_3, \phi_3)$. The steps of the computation are as follows: $$\begin{align} A &= \theta_2 - \theta_1 \\ b &= \phi_2 \\ c &= \phi_1 \\ a &= \cos^{-1} (\cos b \cos c + \sin b \sin c \cos A) &&(1) \\ B &= \cos^{-1} \left( \frac{\cos b - \cos a \cos c}{\sin a \sin c} \right) &&(2) \\ b' &= \cos^{-1} (\cos a' \cos c + \sin a' \sin c \cos B) &&(3) \\ A' &= \cos^{-1} \left( \frac{\cos a' - \cos b' \cos c}{\sin b' \sin c} \right) &&(4) \\ \theta_3 &= \theta_1 + A' \\ \phi_3 &= b' \end{align}$$

Equations (1), (2), (3), and (4) are all by applications of the spherical law of cosines, applied at various vertices of the spherical triangles.

A possible computational problem arises at equations (2) and (4) since there is a potential for division by zero. We can get around this by using the atan2 function available in many libraries of mathematical functions and the identity $$\cos^{-1} \frac{a}{b} = \tan^{-1} \frac{\sqrt{b^2-a^2}}{a}$$ The atan2 function is defined by $\text{atan2(y,x)} = \tan^{-1} (y/x)$, with the difference that the case $x=0$ does not cause an error. Using the identity, (2) becomes $$B = \tan^{-1} \left( \frac{\sqrt{(\sin a \sin c)^2 - (\cos b - \cos a \cos c)^2}} {\cos b - \cos a \cos c} \right) $$ which we might code as

x = cos(b) - cos(a) * cos(c)
y = sqrt(max(0, (sin(a) * sin(c))^2 - x^2))
B = atan2(y, x)

The purpose of the max function in the second line of code above is to guard against the possibility that the argument of the sqrt function might be a small negative number due to round-off in floating point computation in cases where the argument is theoretically zero.

Similarly, for computational purposes we would rewrite (4) as $$A' = \tan^{-1} \left( \frac{\sqrt{(\sin b' \sin c)^2 - (\cos a' - \cos b' \cos c)^2}}{\cos a' - \cos b' \cos c} \right) $$ with computer code similar to the code for (2).

Reference: Wikipedia article on spherical trigonometry

awkward
  • 14,736