Calculate the area of center square in the following figure

Question

Calculate the area of center square in the following figure:(the big square has a side length of 1 and each vertex of big square has been connected to the midpoint of opposite side)
answer choices : $\color{blue}{\frac14 , \frac15 , \frac16 , \frac17 , \frac18}$

Please review and correct my solution:
$$S_{BigSquare}=2S_{BigTriangle}+S_{Paralleogram} \Rightarrow$$ $$S_{Paralleogram}=\frac12 $$
Now let the side lentgh of center square be $x$ , then we have:
$$S_{Paralleogram}=\frac12 =2\times Base\times x =2\times\frac{\sqrt5}{2}\times x \Rightarrow $$
$$x=\frac{\sqrt5}{10} \Rightarrow $$ $$S_{CenterSquare}=\frac{1}{20}$$ ???!!!
Which is not among the choice!!
What's wrong with my solution??!!!

The answer is $1/5$ because each little triangle pairs with an adjacent trapezoid to make a square just like the one in the center. Not an answer because it doesn't explain where you went wrong. — Ethan Bolker, Sep 30 '17 at 16:09
Please define your terms, especially when you’re asking a question. It took me a minute to figure out what you meant by $BigTriangle$ (since, after all, there are *three* differently-sized triangles, and you are referring to the biggest of them). And I’m still not sure what you mean by $Base$. (And, in addition to defining what you mean by that term, you might want to have a separate line showing how you derive its value, as you did for $S_{Parallelogram}$ — which, BTW, you misspelled.) Also, since you’re talking about *area*, you might want to use $A$ rather than $S$. — Scott - Слава Україні, Sep 30 '17 at 20:39
@Scott Sorry,I hadn't enough time to edit the figure and name the vertices... — Hamid Reza Ebrahimi, Oct 01 '17 at 03:25
See also: Area of a square inside a square created by connecting point-opposite midpoint and Finding the area of shaded region. — Martin Sleziak, Nov 16 '17 at 04:23

score 5 · Accepted Answer · answered Sep 30 '17 at 16:14

5

The area of a parallelogram is base $\times$ height, not $2\times$ base $\times$ height.

answered Sep 30 '17 at 16:14

alphacapture

2,981

You're right,so the exact CORRECT answer is $\frac15$.Thank you – Hamid Reza Ebrahimi Sep 30 '17 at 16:20

robjohn · Answer 2 · 2017-09-30T16:32:02.687

My First Approach

The small triangles are $\left(\frac{\sqrt5}{10},\frac{\sqrt5}5,\frac12\right)$ and the big triangles are $\left(\frac12,1,\frac{\sqrt5}2\right)$. Thus, the side of the small square is $$ \frac{\sqrt5}2-\frac{\sqrt5}{10}-\frac{\sqrt5}5=\frac{\sqrt5}5 $$ Thus the area of the small square is $\frac15$.

The Approach in the Question

The area of the parallelogram is $\frac{\sqrt5}2$ (the hypotenuse of the big triangle) times the side of the small square (perpendicular to the hypotenuse). The area of the parallelogram is also $\frac12\cdot1=\frac12$. Thus, we get $$ \frac{\sqrt5}2\cdot\text{side of small square}=\frac12 $$

Thank you.quite right (+1) – Hamid Reza Ebrahimi Sep 30 '17 at 16:24 — Hamid Reza Ebrahimi, Sep 30 '17 at 16:24

score 1 · Answer 3 · answered Sep 30 '17 at 21:13

I'm going to solve this a little different, with a proof.

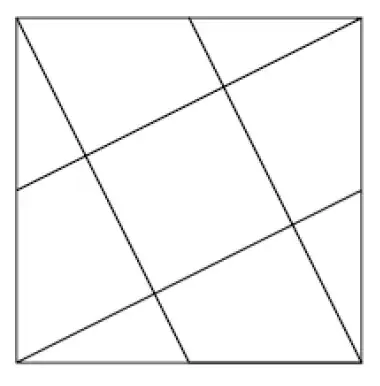
I recreated your pic so I could edit it to show my proof. Also, I'm a little rusty on my proofs and math lingo, so take it easy on me, please.

a' = green triangle b' = red trapezoid d' = blue square

Line a'F equals b'F because it is the same line. Line J equals G because line F bisects the edge of the larger square, as given. The angle between lines E & J is complimentary to the angle between lines G & H. Because of the last line, we know that line H equals 2F. Because of the last line, we can draw another line from the intersection between lines F & G to the intersection between lines B & H and know that it is the same length as line G. From this, we can see that line B equals E. Because of this, line E equals H, so line H equals B. This means b' + a' equals a square of the same volume as d'. As there are 3 more unmarked pairs of a' and b', that means there are a total of 5 equal squares within the original square. This means d' is 1/5 the area of the original square.

Going further: Using parts of the above proof, we can see that a' is 1/4 the area of d'. Which means that b' is 3/4 the area of d'.

I may have skipped parts of the proof, but I considered those parts as "given." I also didn't want to clutter things by trying to prove that all the triangles are the same and that all the trapezoids are the same.

I haven't done a proof in around 20 years, so this proof might not be 100% correct for a proof, but it is correct for the idea.

I don't have enough reputation to post an image, so it's at https://i.stack.imgur.com/ktQLP.png.

Your effort after 20 years is precious:) , +1 – Hamid Reza Ebrahimi Oct 01 '17 at 03:43 — Hamid Reza Ebrahimi, Oct 01 '17 at 03:43

score 0 · Answer 4 · answered Sep 30 '17 at 20:38

By the way, you’re doing an extra step. The area of a parallelogram is the width × the height:

so the area of the parallelogram in the middle of the square is $\frac12\times1 = \frac12$; you don’t need to subtract the area of the big triangles from the area of the big square.

score 0 · Answer 5 · answered Oct 01 '17 at 02:34

0

How is the area of the parellelogram $2bx$? The formula is $bh$, in this case $bx$, giving $$\text{Area}=x^2={1\over 5}$$

answered Oct 01 '17 at 02:34

DynamoBlaze

2,781

Calculate the area of center square in the following figure

5 Answers5

Linked