2

Possible Duplicate:
How come 32.5 = 31.5?

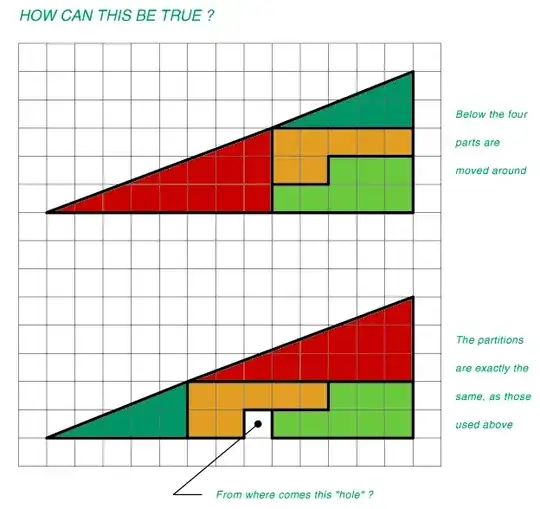
Image

Community
  • 1
0x0
  • 2,641

4 Answers4

10

If you count carefully, you'll see that the base is meant to be $13$ units long, while the height is $5$ units long. That means that the triangle on the top on the top figure, which has a height of $2$, should have a base of length $b$, where $$\frac{b}{2} = \frac{13}{5}$$ or $b = \frac{26}{5}$, longer than the $5$ units depicted.

Likewise, the bottom red triangle, with a base of size $8$ should have a height of length $h$, with $$\frac{h}{8} = \frac{5}{13}$$ or $h = \frac{40}{13}$, which is a little longer than the $3$ depicted.

So in fact, the "missing square" comes from misdrawing the pictures (or from having the individual figures drawn correctly, but the composed figures not being real triangles; the two inner triangles are not similar, though they "should" be).

Ross Millikan
  • 374,822
Arturo Magidin
  • 398,050
2

Eye trick! Look at the angles formed where the red and green triangle meet.

milcak
  • 4,129
  • 1
    Looking at angles may not be enough given the thick lines. But the slope of the hypotenuse of the red triangle is $3/8 = 0.375$ while the slope for the green triangle is $2/5 = 0.4$. If the whole thing was a triangle (which it is not) then the slope would be $5/13 =0.3846\ldots$ – Henry Mar 01 '11 at 23:41
  • Indeed the thick lines are what make the "angles different" - and which is what makes it sloppy. – milcak Mar 01 '11 at 23:47
1

It isn't true. See the Wikipedia page about this puzzle.

Zev Chonoles
  • 129,973
1

Take your credit card, driver's license, or some other readily available straightedge and put it against the hypotenuse. You'll find the composite shape is not a triangle, but a cleverly disguised irregular quadrilateral. The better, more mathy answers made sense once I got my brain away from the idea that there were triangles involved.

Nothing but a cheap trick designed to confound.

djeikyb
  • 201