i want to project an image to four freely positioned points in 2D space. I tried to use perspective and orthogonal transformation, but it hard to wrap my head around it.
I did in photoshop, what i wanted todo programmatically.
Right now i am using an orthogonal projection and in general don't care about the z-axis. Can i do this with a simple matrix transformation and if so, how i can compute this transformation?
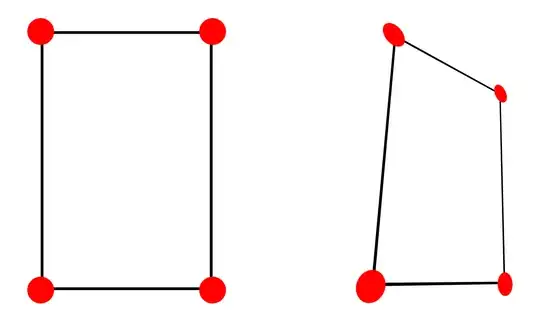
Use a projective transformation defined in this way:
$$\tag{1}\begin{cases}x'=\dfrac{ax+by+c}{gx+hy+i} \\ y'=\dfrac{dx+ey+f}{gx+hy+i}\end{cases}$$
where the 9 coefficients $a,b, \cdots i$ are fixed.
Please note that the denominators are the same.
I advise you to take at first, for example
small values $g=h=0.1$ or $0.2$ and always $i=1.$
$a=1, b=0.2, c=0, d=0.2, e=1, f=0$.
In this way you will not be too far from an affine transform. Increasing the values of $g$ and $h$ will accentuate the perspective.
If you want to build a projective transform that maps four given points onto four other given points, and assuming that $i=1$, as you have to know 8 coefficients $a,b,... h$, the count is good: you have to right down equations (1) four times, one for each $(x_k,y_k)$ and the corresponding image $(x'_k,y'_k)$. This generates 8 equations with 8 unknowns which, once solved give the unknowns $a,b,... h$.
