Godel's Diagonalization Lemma As Application Of Lawvere's Fixed Point Theorem

Question

I've read through this paper with applications of Lawvere's fixed point theorem. On the diagonalization lemma, they say the following:

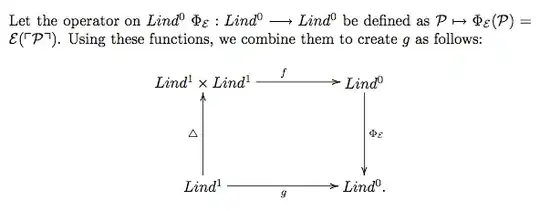
For one thing, how can $f$ and $\Phi_{\cal E}$ be well defined maps? As far as I understand, the Lindenbaum algebras contain all FO formulas in the language of some theory $S$, modulo $S$-equivalence (logical equivalence proveable from $S$). And this also makes sense, since the fixed point we ought to find is only fixed modulo $S$-equivalence, but I don't see $f$ and $\Phi_{\cal E}$ factorizing through $S$-equivalence.

Also, am I right to interpret the arrows here not as algebra homomorphisms but set functions?

Here's what I've tried so far to save the proof:

• First I define $\ulcorner\phi\urcorner_S$ to be the smallest number $n$ such that $S\vdash\phi\longleftrightarrow\llcorner n\lrcorner$

• Then I show that the diagonalization lemma $\forall{\cal E}\in\text{Lind}^1_S.\exists{\cal C}\in\text{Lind}^0_S.S\vdash{\cal C}\longleftrightarrow{\cal E}(\ulcorner{\cal C}\urcorner)$ is weaker than its variant using $\ulcorner\cdot\urcorner_S$ instead of $\ulcorner\cdot\urcorner$.

• I define $f'$ and $\Phi'_{\cal E}$ as the $\ulcorner\cdot\urcorner_S$-variants of $f$ and $\Phi_{\cal E}$ respectively.

• Then I show that $f'$ and $\Phi'_{\cal E}$ factorize through $S$-equivalence and that $\Phi'_{\cal E}\circ f'\circ\Delta$ can be encoded over $f'$, i.e. there exists $[\phi]\in\text{Lind}^1_S$ such that $\Phi'_{\cal E}\circ f'\circ\Delta=f'\circ({\sf id}\times{\sf c}_{[\phi]})$ (where ${\sf c}_x$ denotes the constant map to $x$).

At this point I can safely apply Lawvere's fixed point theorem to get the $\ulcorner\cdot\urcorner_S$- variant of Godel's diagonalization lemma.

[EDIT] Let's say we want to prove the diagonalization lemma over some theory $T$ in a (possibly weaker) theory $S$. Intuitively it seems to me that very weak $S$ (Weaker than PA) might not prove the $\ulcorner\cdot\urcorner_T$-version of the lemma. Since I feel that for the original lemma I only need to formulate the halting problem (will program $n$ on input $m$ halt) but for the $\ulcorner\cdot\urcorner_T$-version I might need to formulate something like what is the smallest $m$ such that program $n$ halts on $m$. Could there be some truth to this?