Here's a list of the $x$ in the fundamental solution of $x^2-dy^2=1$. It seems when $d=n^2-3$ for an integer $n$ the $x$ is often quite large. Is this a coincidence or is there an explanation?
For $n>5$ the continued fraction of $\sqrt {n^2-3}$ starts with $$\sqrt {n^2-3} = \left[n-1;1,n-2-\lfloor n/3\rfloor, a_n...\right]$$ Where $a_n=3$ if $n\equiv 2\pmod 3$ and $1$ otherwise. Maybe this is related.
When $n$ is a multiple of 3, the solution is small because $(6n^2-1)^2-(9n^2-3)(2n)^2=1$.
In this file the $n$th line is the continued fraction of $\sqrt{(3n+1)^2-3}$. There are some interesting patterns in it, for example in the 12th column there seems to be a pattern repeating mod 9: $13,1,1,1,1,1,2,3,5$. Here's the same thing for $\sqrt{(3n+2)^2-3}$.
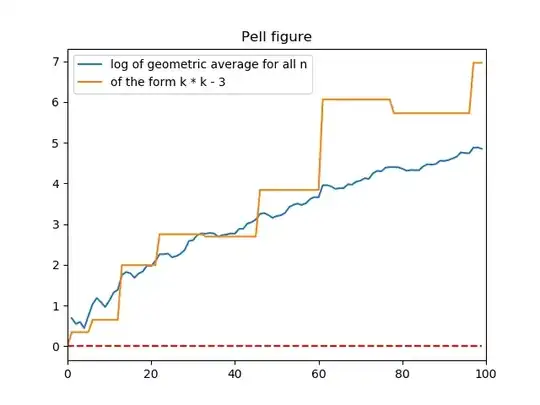
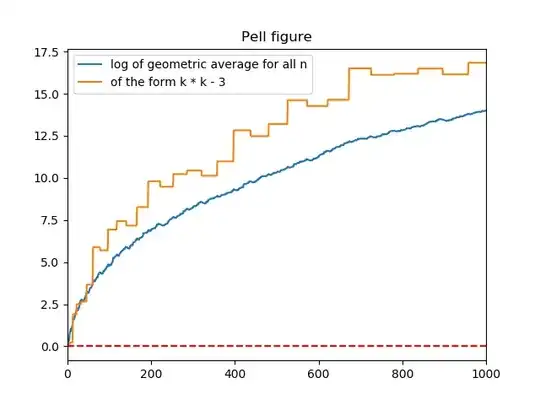

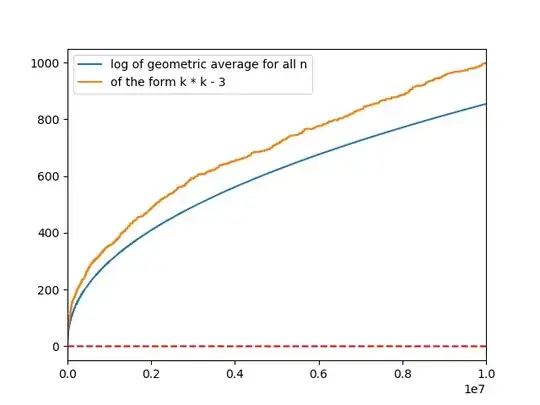
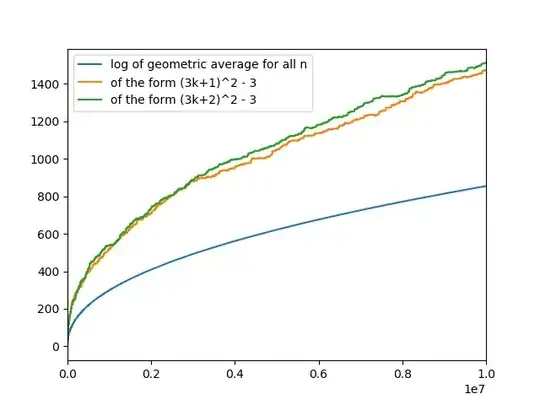
Here the blue line is the log of the geometric average of the x in the minimal solution of the pell equation and the orange line is that only for numbers of the form $n^2-3$. Eyeballing that last plot $$\ln\left(\left(x_1x_6x_{13}\dots x_{9998241}\right)^{1/3162}\right)\approx\ln\left(\left(x_1x_2x_3\dots x_{10^7}\right)^{10^{-7}}\right) + 150$$ $$(x_1x_6x_{13}\dots x_{9998241})^{1/3162}\approx e^{150}(x_1x_2x_3\dots x_{10^7})^{10^{-7}}$$ Where $(x_n, y_n)$ is the fundamental solution of $x^2-ny^2=1$, when $n$ is a square I set $x_n=1$. Also, the geometric average of the subsequence is higher than the average of the whole sequence for all $61\leq n < 10^7$.
Exluding the cases where n is a multiple of 3 makes the effect even larger: