Simplify $\sin{(\arctan{2}-\arcsin{\frac{1}{\sqrt{10}}})}.$

Question

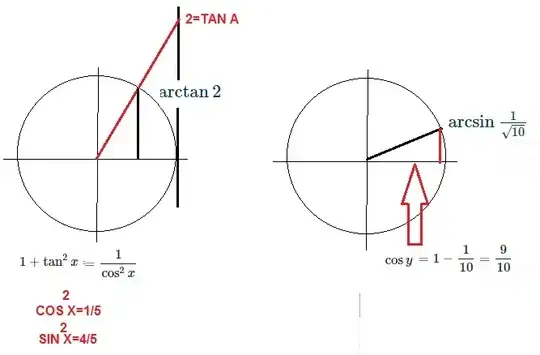
First I denote $x=\arctan{2}$ and $y=\arcsin{\frac{1}{\sqrt{10}}}$ and then use the addition formula for sine:

$$\sin{(x-y)}=\sin{x}\cos{y}-\cos{x}\sin{y}=\sin{x}\cos{y}-\cos{x}\cdot \frac{1}{\sqrt{10}}.$$

Now I use the fact that $\cos{y}=1-\sin^2{y}$ which gives

$$\cos{y}=1-\sin^2{\left(\arcsin{\frac{1}{\sqrt{10}}}\right)}=1-\frac{1}{10}=\frac{9}{10}$$

So I have reduced the problem to the following

$$\sin{x}\cdot \frac{9}{10}-\cos{x}\cdot \frac{1}{\sqrt{10}}.$$

Here I'm stuck. I cant just divide this expression by $(\sin{x}\cos{x})$ because I'd still be left with sine and cos terms and I'd also change the value of the expression. Everything now boils down to compute $\sin(\arctan{2})$ and $\cos{\arctan2}.$ I also tried rewriting $\cos(\arctan{2})$ as $1-\sin^2(\arctan{2}),$ but to no avail.

Any suggestions on

1. how to proceed from where I left;
2. how tocompute this by means more effective;
3. both of the above.

Answer 1

Was going to leave a comment on GAVD's answer, but it's not difficult to do with

$$\sin(\arctan(x)) = \frac x {\sqrt{x^2 + 1}}$$

Which you can prove using,

$$1 + \cot^2(\arctan(x)) = \csc^2(\arctan(x))$$

By the Pythagorean identity. From which,

$$1 + \frac 1 {x^2} = \frac{1}{\sin^2(\arctan(x))}$$ $$\frac {x^2} {x^2+1} = \sin^2(\arctan(x))$$

Taking square roots, choosing the positive branch,

$$\frac x {\sqrt{x^2 + 1}} = \sin(\arctan(x)) \blacksquare$$

Answer 2

Put $\arctan 2 = x$ then $\tan x= 2$, so $\sin x = {2\over \sqrt{5}}$ and $\cos x = {1\over \sqrt{5}}$.

Let $\arcsin {1\over \sqrt{10}}= y$ so $\sin y = {1\over \sqrt{10}}$, thus $\cos y = {3\over \sqrt{10}}$.

Now:

$$\sin{(\arctan{2}-\arcsin{\frac{1}{\sqrt{10}}})} = \sin (x-y) = \sin x \cos y- \cos x \sin y= {\sqrt{2}\over 2} $$

Answer 3

Hint:

$\frac{\sin x}{\cos x} =\tan(x)=2$ and $\sin^2x+\cos^2x=1$

Answer 4

Hint:

$$\sin x =\sqrt{1-\cos^2 x} =\sqrt{1-\frac{1}{1+\tan^2 x}} $$

$$\cos x =\sqrt{\frac{1}{1+\tan^2 x}} $$ Since

$$ 1+\tan^2 x =1+\frac{\sin x^2}{\cos^2 x} = \frac{\cos^2x+\sin x^2}{\cos^2 x} =\frac{1}{\cos^2 x}$$

Answer 5

HINT: $$\sin(\arctan x) = \frac{x}{\sqrt{1+x^2}}.$$

EDIT 1: Prove the hint. Let $u = \arctan x$, then $x = \tan u$.

So, we have $$\frac{x}{\sqrt{1+x^2}} = \frac{\tan u}{\sqrt{1+\tan^2 u}} = \tan u \cos u = \sin u = \sin( \arctan x).$$

Answer 6

$x=\arctan 2$ means $\tan x=2$ thus

$\sin x = \dfrac{\sqrt{\sin^2 x}}{\sqrt{1}}=\dfrac{\sqrt{\sin^2 x}}{\sqrt{\sin^2 x+\cos^2 x}}=\dfrac{\sqrt{\frac{\sin^2 x}{\cos^2 x}}}{\sqrt{\frac{\sin^2 x}{\cos^2 x}+\frac{\cos^2 x}{\cos^2 x}}}=\dfrac{\tan x}{\sqrt{\tan^2 x+1}}$

$\sin x=\dfrac{2}{\sqrt 5}$ and $\cos x =\sqrt{1-\sin^2 x}=\dfrac{1}{\sqrt 5}$

$y=\arcsin \dfrac{1}{\sqrt{10}}$ means $\sin y=\dfrac{1}{\sqrt{10}}$ and $\cos y=\sqrt{1-\sin^2 y}=\dfrac{3}{\sqrt{10}}$

Therefore $\sin{\left(\arctan{2}-\arcsin{\frac{1}{\sqrt{10}}}\right)}=\sin(x-y)=\sin x\cos y -\cos x\sin y=$

$=\dfrac{2}{\sqrt 5}\cdot \dfrac{3}{\sqrt{10}}-\dfrac{1}{\sqrt 5}\cdot \dfrac{1}{\sqrt{10}}=\dfrac{5}{\sqrt{50}}=\dfrac{5}{5\sqrt 2}=\dfrac{1}{\sqrt 2}$

Answer 7

$$\sin{(\arctan{2}-\arcsin{\frac{1}{\sqrt{10}}})} = \\\sin (x-y) =\\ \sin x \cos y- \cos x \sin y= \frac{2}{\sqrt 5}.\frac{3}{{\sqrt {10}}}-\frac{1}{\sqrt 5}.\frac{1}{{\sqrt {10}}}\\=\\\frac{6-1}{\sqrt{50}}=\frac{1}{\sqrt2} \to x-y=\frac{\pi}{4}$$

Answer 8

If $t=\arcsin\dfrac1{\sqrt{10}},0<t<\dfrac\pi2$

$\sin t=\dfrac1{\sqrt{10}},\tan t=+\dfrac{\sin t}{\sqrt{1-\sin^2t}}=\dfrac13$

$\implies t=\arctan\dfrac13$

Now $\arctan2-\arctan\dfrac13=\arctan\dfrac{2-\dfrac13}{1+\dfrac23}=\dfrac\pi4$