intersection of continuous curves in a square.

Question

I dont really need this result, but I'm very curious what the answer is and was thinking about it for quite a while without anything productive, so I'd be grateful if someone here could indulge my curiosity.

Let ABCD be a square in a Euclidean plane. Let a and b be two continous curves inside the square, such that a goes from A to C (diagonally opposed poonts) and b from B to D. Show that a and b have at least one point of intersection.

I'm not even sure if the result is correct, but intuitively on drawings it seems it must be true.

Answer 1

The claim is indeed correct.

The only really solid proof I can think of uses Alexander Duality from algebraic topology, and I suspect that this is not likely to be satisfactory to you, as you may not know that theorem or have ever studied topology.

If you're willing to say that the curves $a$ and $b$ are not merely "continuous" but "nice" (e.g., neither one is a space-filling curve, for instance, and neither one is self-intersecting (like the letter $\alpha$), then there might be a simpler proof, but even in this simpler case, I cannot really think of one.

Well...here's a kind of proof, assuming you know how to compute integrals. Put the square with $A$ at the origin of the plane, $B$ to the right, along the $x$ axis, and $D$ above, on the $y$ axis. Now add to the curve $b$ the 3/4 arc of a circle from $D$ to $B$, as in this picture: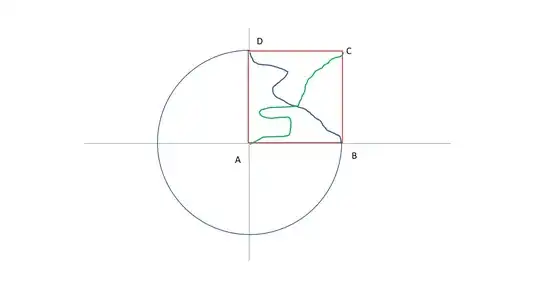

You can now take the entire blue curve, which is a loop, agree to traverse it counterclockwise, and compute its winding number around the point $A$ by writing down an integral (see Wikipedia for what integral defines the winding number). Because all along the curve $b$, the angle from $A$ is in the first quadrant, it's not too hard to show that this winding number is $1$.

On the other hand, if you compute the winding number around the point $C$, it turns out to be $0$, for similar reasons.

For each point $u$ of the curve $a$, you could similarly compute the winding number around $u$. Then you have to show that if $u$ is never a point of $b$, that this winding number is a continuous function of the location of $u$. That requires some calculus, probably Leibniz' theorem.

Finally, suppose that curves $a$ and $b$ do not intersect. Then the winding number $w(u)$ is a continuous function of $u$ as $u$ moves from $A$ to $C$, but this continuous function is $1$ at $A$ and $0$ at $C$, and takes on only integer values. That is a contradiction, and hence the assumption that they don't intersect must be wrong.

This proof relies on $b$ being a nice enough curve that you can compute the winding number using integration; I'm not certain, but I suspect that "continuous" is probably enough, but I've been fooled before. It also depends on the continuity of integrals like the winding number with respect to the parameters like the center point around which the integral is computed -- that's messy calculus.

Still, this is at least a sketch of a solid non-algebraic-topology proof.

** Post-comment addition **

To give an algebraic-topology based proof sketch, consider the (filled in) square as a disk in the plane, and $A, B, C, D$ as four points on the boundary circle, say at $\theta = 0, \pi/2, \pi, 3\pi/2$.

Treat this disk as the upper hemisphere of $S^2$. Take the arc $a$ from $A$ to $C$, and adjoin to it the great semicircle containing $A, C,$ and $S$, where $S$ is the south pole. Call this set --- which is just the image of a circle mapped to $S^2$ --- by the name $X$, and call its complement $Y$.

Then Alexander duality tells us that $H^{n-q-1}(Y)$ is isomorphic to $H_q(X)$, where $n = 2$ is the dimension of the sphere in which $Y$ lives, i.e., that $$ H^{q-1}(Y) = H_q(X) $$ and where $H$ denotes reduced homology or cohomology.

Now $H_1(X)$ certainly contains a copy of $\Bbb Z$ corresponding to "go once along $a$ and then continue along the great semicircle, returning to where you began." That means that $H^{0}(Y)$ contains a copy of $\Bbb Z$, which is to say that the non-reduced cohomology of $Y$ contains two copies of $\Bbb Z$, hence that $Y$ has two connected components. And that's really the essence of the thing.

I suspect that the version of Lefschetz duality that works on triples rather than pairs could do this somewhat more simply, but I don't have the wit to see how.

Answer 2

Here's a proof that only uses basic topology. Claims 1 and 2 below can be skipped if you happen to know about the lifting theorem.

Let's call $C=[0,1]^2$ and $S^1$ the unit complex circle. I will identify $\mathbb R^2$ with $\mathbb C$ the usual way, so $C$ can be seen as the square in the complex plane whose vertices are $0,1,1+i,i$. So we have two continuous $\gamma_{1,2}:[0,1]\to S^1$ functions, with, say, $$\gamma_1(0)=0,\ \gamma_1(1)=1+i$$ $$\gamma_2(0)=1,\ \gamma_2(1)=i$$ Assume they don't cross, ie $\gamma_1(t)\neq\gamma_2(u)$ for all $(t,u)\in[0,1]^2$. For convenience we'll identify $(t,u)$ with $z=t+iu\in C$. Under our hypothesis, we can define the following $C\to S^1$ continuous mapping $$f(z)=\frac{\gamma_2(u)-\gamma_1(t)}{|\gamma_2(u)-\gamma_1(t)|}$$ (the unit vector from the point of $\gamma_1$ of parameter $t=\mathrm{Re}~z$ to the point of $\gamma_2$ of parameter $u=\mathrm{Im}~z$).

We now proceed to show that there exists $\varphi:C\to\mathbb R$ continuous, such that $f=e^{i\varphi}$ identically (of course, if it weren't for the continuity the existence would be obvious). If $D$ is any subset of $\mathbb C$, we'll say that $\varphi$ is a lifting of $f$ over $D$ if $\varphi$ is continuous and $f=e^{i\varphi}$ identically over $C\cap D$.

Basically, we show that $f$ is locally liftable, then proceed to merge local liftings, which only takes a finite number of steps thanks to compacity, and ends due to connectedness.

Claim 1 : for any $z_0\in C$, there is $\eta>0$ and $\varphi_0$ that lifts $f$ over $D(z_0,\eta):=\{z\in\mathbb C\mid~|z-z_0|<\eta\}$.

Proof. Take a disk $D_1$ around $f(z_0)$, small enough so that the real part of $g(z)=\frac{f(z)}{f(z_0)}$ is $>0$ whenever $f(z)\in D_1$ ; for instance, $D_1=D(f(z_0),1)$. By continuity, there is $\eta>0$ and $D=D(z_0,\eta)$ such that $f(z)\in D_1$ for all $z\in C\cap D$. Over this set the principal argument $\theta(z)$ of $g(z)$ stays in $(-\pi/2,\pi/2)$, so that $$\theta(z)=\tan^{-1}\frac{\mathrm{Im}~g(z)}{\mathrm{Re}~g(z)}$$ is a continuous function of $z$. Now take $\theta_0$ to be any argument of $f(z_0)$, then $$\varphi_0:C\cap D\to\mathbb R\ ,\ z\mapsto\theta_0+\theta(z)$$ is easily seen to be a lifting of $f$ over $D=D(z_0,\eta)$. $\square$

Claim 2 : there is a lifting $\varphi$ of $f$ over $C$.

Proof. When $z$ ranges over $C$, the $D(z,\eta(z))$ from the previous claim form an open covering of $C$, from where, by compacity, we can extract a finite subcovering $$C\subset\bigcup_{k=1}^n D(z_k,\eta_k)\quad,$$ each $D_k=D(z_k,\eta_k)$ coming with its own lifting $\varphi_k$. Since $C$ is connected and each disk has a non empty intersection with $C$, the $D_k$'s are not pairwise disjoint, so say for instance $D_1\cap D_2\neq\varnothing$. Over this intersection, we have $e^{i\varphi_1}=e^{i\varphi_2}$ identically, so that $\varphi_2(z)=\varphi_1(z)+2h(z)\pi$, where $h:D_1\cap D_2\to\mathbb Z$. But since $\varphi_{1,2}$ are continuous, $h$ must be a constant $h_0$, and it is clear that $\varphi_2-2h_0\pi$ is still a lifting of $f$ over $D_2$. Since it agrees with $\varphi_1$ over the intersection, we can use it to extend $\varphi_1$ to a lifting over $D_1\cup D_2$. Here, it is immaterial that $D_{1,2}$ are disks, so this process of "merging the liftings" can be carried over until we obtain one global lifting over $C$ (by $C$'s connectedness, we cannot be stuck at a point where two subcoverings wouldn't intersect). $\square$

Now that we have a lifting $\varphi$ of $f$ over $C$, it is easily seen that $\psi$ is a lifting if and only if $\psi=\varphi+2h\pi$, identically, for some constant $h\in\mathbb Z$. Since $f(0)=1$, we can arbitrarily choose $\varphi(0)=0$, thus entirely characterizing $\varphi$. Now make $u$ range continuously from $0$ to $1$, while $t=0$. Then $f(z)=f(t+iu)=$ $=f(i)=i$, so that $\varphi(i)\equiv\pi/2\pmod{2\pi}$, but $f$ stays in the first quadrant during the whole process, hence $\varphi(i)=\pi/2$. Likewise, from that point on, make $t:0\to 1$, then $u:1\to 0$, then finally $t:1\to 0$. Accordingly, you get $\varphi(1+i)=\pi,\varphi(1)=3\pi/2$ and $\varphi(0)=2\pi$. This is in flagrant contradiction with $\varphi(0)=0$, and so we conclude that $f$ is ill defined, ie, the curves must intersect.

Answer 3

A graph\picture is at the bottom of this answer.

Lemma 1: Let $C \subset \mathbb R \times \mathbb R$ be a connected subspace containing both the points $(-1,0)$ and $(+1,0)$.
Then $C$ must have a nonempty intersection with the $y\text{-axis}$.
Proof: Exercise.

If we modify the $y\text{-axis}$ by changing the line segment connecting both $(0,+1)$ and $(0,-1)$ into a polygonal chain contained inside the blue square, lemma 1 will still be true.

Definition/Notation: Let $K$ be a compact connected set contained in the square and containing exactly two points from the perimeter of the square - $(0,+1)$ and $(0,-1)$. Then $K$ is called a distortion of the $y\text{-axis}$, and we denote by $K^{'}$ the union of $K$ with the line segment $(0,+1)\text{-UP}$ and the line segment $(0,-1)\text{-DOWN}$.

Assume now that the $C$ described in lemma 1 is also a closed subset of $\mathbb R \times \mathbb R$.

Proposition 2: $C \cap K^{'} \ne \emptyset$.
Proof
Suppose $C$ has an empty intersection with $K$. For each point in $K$ except for the 'end points', choose an open ball inside the blue interior of the square that does not intersect $C$. Do the same thing at the points $(0,+1)$ and $(0,-1)$; observe that for those two points, you get a disc wedge in the subspace topology on the square.

We choose a finite sub-cover of $K$. Starting at $(0,+1)$, there must be a polygonal chain inside the blue interior connecting it to $(0,-1)$. Each open ball intersects another open ball, and we construct line segments from the centers of the discs. An 'island of open balls' would mean that $K$ is not connected.

By construction, this linear chain does not intersect $C$. But then $C$ must intersect with $K^{'}$ outside the square. $\qquad \blacksquare$

Here is the reference graph: