Fixing a wobbly table - Revisited

Question

There is this video on the Youtube channel Numberphile in which it is argued that each wobbly four legged square table can be made stable by just minor adjustments in position, namely an at most $90^°$ turn around its center.

Too long to read: I doubt the completeness of the presented solution. Hence I am not sure if every table can be stabelized in the demonstrated way. Of course Numberphile is a popular math channel and cannot go into much detail, but I think there might be much more than just some simple gap filling and formalization work to complete the proof.

Question: Is the problem indeed harder than demonstrated in the video? Or is the solution complete and I can just not see how? How to fix it otherwise?

---

There were some assumptions made and I will start here with formalizing the problem. At first, I assume that the ground on which the table is placed is given as a continuous function $f:\Bbb R^2\to\Bbb R$. For some point $(x,y)=p\in\Bbb R^2$ I will write $\bar p:=(x,y,f(p))\in\Bbb R^3$ for its lifting onto the ground in three dimensions.

Now the problem of finding a stable position for the table can be given as follows:

Conjecture. Given a continuous function $f:\Bbb R^2\to \Bbb R$. There are four points $(x_i,y_i)=p_i\in\Bbb R^2,i=1,2,3,4$ so that the points $\bar p_i$ form a unit-square.

However, the demonstrated solution of the problem in the video aims for a stronger statement. For this, call a set $\{p_i\}$ of points $p_i\in\Bbb R^2,i=1,2,3$ squarable if there is a point $\diamond(p_i)\in\Bbb R^3$ so that $$\{\bar p_1,\bar p_2,\bar p_3,\diamond(p_i)\}$$ form the corners of a unit-square. So the video states

Conjecture. Given a continuous function $f:\Bbb R^2\to \Bbb R$ and a squarable set $\{p_i^0\}$ of three points $p_i^0\in\Bbb R^2,i=1,2,3$. Then there are continuous functions $p_i:[0,1]\to\Bbb R^2,i=1,2,3$ so that

1. it holds $p_i(0)=p_i^0$,
2. the set $\{p_i(t)\}$ is squarable for all $t\in[0,1]$,
3. there is a point $p_4\in\Bbb R^2$ with $\bar p_4=\diamond(p_i(1))$.

Stated informally this means that a table in a possibly wobbly initial position (see 1.) can be moved continuously (see 2.) into a stable position (see 3.).

Now the video explains how to choose the paths $p_i(t)$ in a clever way, so that 3. is satisfied automatically by the intermediate value theorem. In detail, they choose path $p_i(t),i=1,2,3$ to start in $p_i^0$ and aim for $p_{i+1}^0$ (assume $p_4^0$ is the projection of $\diamond(p_i^0)$ into the plane). They call this a rotation of the table around its center. Then they argue that condition 3. is satisfied for some time $t\in[0,1]$.

I do not have any objections against this latter argument. I just realized that they completely skipped to argue that such paths even exist! In the end, condition 2. is a strong restriction and the existence is not obvious.

---

The rest of this post contains some arguments with which I convinced myself that the problem might be non-trivial.

At first I went one diemnsion lower. I tried to move a two dimensional table along a function-graph by keeping the legs on the ground. I asked: is it always possible to move the table from the left to the right without loosing touch with the ground?

Lets formalize this. Again the ground is a continuous function $f:\Bbb R\to\Bbb R$. A point $p\in\Bbb R$ is lifted to $\bar p=(p,f(p))\in\Bbb R^2$. Instead of a unit-square, here we have to keep the touching point of the legs with the ground in the form of a unit interval, i.e. at distance one.

Question: Given a continuous function $f:\Bbb R\to\Bbb R$ and $x_0,x_1,y_0\in\Bbb R$ with $\|\bar x_0-\bar y_0\|=1$. Are there continuous functions $x,y:[0,1]\to\Bbb R$ so that

1. it holds $x(0)=x_0$, $y(0)=y_0$ and $x(1)=x_1$,
2. it holds $\|\bar x(t)-\bar y(t)\|=1$ for all $t\in[0,1]$.

Looking at the above sketch, this might seem trivial. However, when we choose functions like $f(x)=100 \sin(x^2)$ and want to move the table from $x_0=0$ to $x_1=100$, it is not clear that this can be done. Try it! I will now demonstrate you my approach to solve this question and the problems I encountered on the way.

Define the function $d(x,y):=\|\bar x- \bar y\|$. Note that $d$ is a function $\Bbb R^2\to\Bbb R$, hence describes a height map over a two-dimensional area. The $x(t)$ and $y(t)$ in the above formulation are the positions of the table legs at each point in time. Condition 2. is then equivalent to $d(x(t),y(t))=1$. Hence we are interested in paths of constant "height 1" in the height map given by $d$.

For example, the following figure shows on the left a plot of $f(x)=2\sin(x^2)$, and on the right the associated hightmap. The black points are all the points with $d(x,y)=1$.

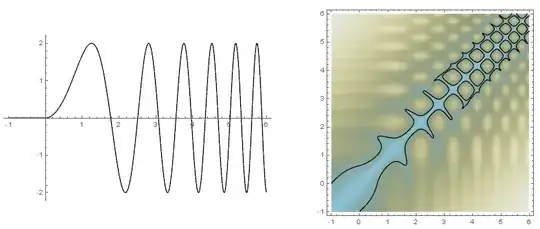
It looks pretty complicated. But the good thing is that there is indeed a path (the black curve) connecting the bottom of the plot with the top. The $x$- and $y$-coordinates of this path are the desired $x(t)$ and $y(t)$ functions of how to move the tables legs. The hard part is to show that such a path exists always. I tried to show this using some generalizations of the intermediate value theorem but there are sitations where this approach fails. And I was not able to proof that such situations cannot occure for this problem.

The second observations are the closed loops in the right figure. They indicate positions in which the table can be placed, but from which he cannot escape. This was strong evidence for me that the problem is highly non-trivial. How do I know that such locked situations do not occure in the case of a square table? Why should I be able to rotate the table while keeping the legs on the ground? What if I am in such a separate connected component as in the above simplified problem?