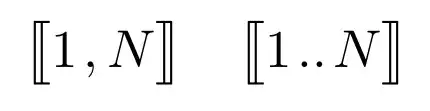Is there a special symbol for the set: $$ \{1, 2, 3, \dots, n\}$$, or $$\{x| 1\leq x\leq n, n \in \mathbb{Z} \} $$?
Asked
Active
Viewed 9,894 times
7
-
in which context are you going to use it? – trying Sep 11 '17 at 08:07
-
3Some people use $[n]$ to refer to this. Other people use $[n]$ to refer to ${0,1,2,3,\dots,n-1}$. In both cases it is intended for $[n]$ to be of cardinality $n$ and the distinction often doesn't need to be explicitly made (e.g. Suppose that $|A|=n$, then there exists a bijection from $A$ to $[n]$) – JMoravitz Sep 11 '17 at 08:11
-
@trying, the problem arises from https://math.stackexchange.com/questions/2385152/denote-the-elimination-of-the-row-and-the-column-corresponding-a-matrix-element – whitegreen Sep 11 '17 at 08:14
-
ok, but where in that problem you want to make use of ${0,1,2,...,n-1}$ (for which you searching for a shorter symbol)? give an example of a statement, where you want to use it – trying Sep 11 '17 at 08:24
-
If you want to simplify the notation for the expanded form of matrix you can use $A=\begin{Vmatrix}a_{i,j}\end{Vmatrix}^n_1$ – trying Sep 11 '17 at 08:34
-
@JMoravitz It seems to me that a name for the set ${1,2,3,\dots,n}$ would be more useful than another name for the set ${0,1,2,\dots,n-1}$ which already has a concise name, namely $n.$ – bof Sep 11 '17 at 09:25
-
1@bof that line of conversation has already been had on the linked question. As for why we don't use $n$ to denote ${0,1,\dots,n-1}$ I would think it avoids possible confusion in needing to remind the reader that $n$ the natural number is formally defined as a set in the first place, especially when it isn't perfectly clear that we are referring specifically to $n$ the natural number rather than $n$ the positive integer or $n$ the real number which happen to be equivalence classes of their respective objects (e.g. cauchy sequences). Adding merely two brackets avoids any such confusion. – JMoravitz Sep 11 '17 at 15:47
-
1@bof: That's a bad idea because it is better to separate the abstraction from the implementation. It makes no sense to use $n = {0,1,...n-1}$ in any context whatsoever except when showing that there is a model of PA, or when dealing with ordinals. In every other context all we need is a model of PA, and so it would be wrong to have that equality because we want our theorem and proof to not depend on the chosen model of PA. It is the same with real analysis, where you ought to be proving theorems about any model of the second-order axiomatization of the reals. – user21820 Dec 08 '19 at 10:10
-
@JMoravitz: Besides what I said in my previous comment, I would also say that it is not accurate to say that natural numbers are "formally defined as sets in the first place", as that is merely one possible choice of many, and it is even arguable that other choices are better. For example, there is no philosophical reason to stipulate that every object is a set, so the abstract natural numbers too are not necessarily sets. As in my previous comment, all that matters is that there is a model of PA, not what the elements in that model are. – user21820 Dec 08 '19 at 10:16
-
In fact, the one who came up with the notion of well-foundedness of sets did not consider it to be satisfied by all sets, and indeed ZFC minus Foundation is compatible with urelements and yet is as strong as ZFC. – user21820 Dec 08 '19 at 10:20
3 Answers
3
Bernard
- 175,478
-
Really? Where did your find this? Especially here at mathexchange it would be useful to present this by LaTex and not by a picture. – miracle173 Sep 11 '17 at 08:48
-
@miracle173: I made it in LaTeX, but MathJax doesn't have the tools for that (fitting the standard fonts, you have to load
stmaryrdand use\llbracket/\rrbracket, but several other packages have similar symbols – among whichfourier). – Bernard Sep 11 '17 at 09:34 -
-
1@miracle173: You can just write "$[1..N]$" after defining it. I see no reason to use the fancy brackets when it is already clear as day what it means. It is also used in many many programming-related writings especially for array indices. – user21820 Dec 08 '19 at 10:03
3
Some people use $$\mathbb{N}_k = \{1, 2, \ldots, k\}$$
mechanodroid
- 46,490
-
1Sometimes $\mathbb{N}_0$ is used to denote the natural numbers including zero, so this notation may be ambiguous. – Epiousios Sep 11 '17 at 09:04
0
Consider that for positive reals the standard symbol, as Wikipedia says, is $\mathbb{R}_{>0}$
Then I think that you can use the following symbol for $\{1,2,...,n\}$ $$\mathbb{N}_{\le n}$$
trying
- 4,756
- 1
- 13
- 23
-
1In most modern branches of mathematics, $0 ∈ \mathbb{N}$, so this isn't a good answer. Moreover, it is bad from a design perspective because most places where it is convenient to use "$[1..n]$" it is often also convenient to use other integer ranges like $[m..n]$ or $[-n..n]$. – user21820 Dec 08 '19 at 10:05