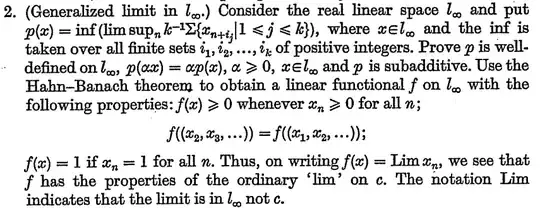Generalized limit in $l_\infty$ (Using: Hahn Banach Extension Theorem)

Question

I am trying to solve the following problem (found in Maddox's book "Elements of Functional Analysis", page 128):

So we have the function $p:l_\infty\rightarrow\mathbb{R}$ given by

$$ p(x) = \inf\left\{\limsup_{n\rightarrow\infty}\left(\frac{1}{k}\sum_{j=1}^k x_{n+i_j}\right) \right\} $$

In which the infimum is taken over all finite sets of positive integers $\{i_1,\ldots,i_k\}$.

I already showed that:

• $p$ is well defined in $l_\infty$
• $p(\alpha x)=\alpha p(x)$, for all $x\in l_\infty$ and $\alpha >0$
• $p$ is subadditive, i.e $p(x+y)\leq p(x)+p(y)$, for all $x,y\in l_\infty$

This part I'm not sure that it's the best way to do it:

To obtain a functional as the problem states, I defined first another functional $g:c\rightarrow \mathbb{R}$ ($c$={space of convergent sequences}), given by:

$$ g((x_n)_n) = \lim_{n\rightarrow\infty} x_n $$

It was not difficult to show that:

• $g$ is linear
• $g(x)\leq p(x)$, for all $x\in c$. (Actually we'll have $g(x)=p(x)$)
• $g((1,1,1,\ldots))=1$

Now, the Hahn Banach Extension Theorem states that there is a functional $f:l_\infty\rightarrow \mathbb{R}$ such that:

• $f(x)=g(x)$, for all $x\in c$
• $f(x)\leq p(x)$, for all $x\in l_\infty$

Now I just have to show that $f$ satisfies the conditions given by the problem, which are:

1. $f(x)=1$ if $x_n= 1$ for all $n$
2. $f(x)\geq 0$ if $x_n\geq 0$ for all $n$
3. $f((x_2,x_3,\ldots))=f((x_1,x_2,\ldots))$

(1) is straightforward, since the condition is valid for $g$.

My Difficulties:

(2) I managed to demonstrate this one, but I'm not sure I'm correct, this is my solution:

For every $x\in l_\infty$ we have

$$ f(x) \leq p(x) = \inf\left\{\limsup_{n\rightarrow\infty}\left(\frac{1}{k}\sum_{j=1}^k x_{n+i_j}\right) \right\} $$

So we have

\begin{align} -f(x) = f(-x) \leq p(x) &= \inf\left\{\limsup_{n\rightarrow\infty}\left(\frac{1}{k}\sum_{j=1}^k (-x_{n+i_j})\right) \right\}\\ &= \inf\left\{\limsup_{n\rightarrow\infty}\left(-\frac{1}{k}\sum_{j=1}^k x_{n+i_j}\right) \right\}\\ &= \inf\left\{-\liminf_{n\rightarrow\infty}\left(\frac{1}{k}\sum_{j=1}^k x_{n+i_j}\right) \right\}\\ &= -\sup\left\{\liminf_{n\rightarrow\infty}\left(\frac{1}{k}\sum_{j=1}^k x_{n+i_j}\right) \right\} \end{align}

From which we get

$$ f(x) \geq \sup\left\{\liminf_{n\rightarrow\infty}\left(\frac{1}{k}\sum_{j=1}^k x_{n+i_j}\right) \right\} $$

And clearly if $x_n\geq 0$ for all $n$, then

$$ f(x) \geq \sup\left\{\liminf_{n\rightarrow\infty}\left(\frac{1}{k}\sum_{j=1}^k x_{n+i_j}\right) \right\} \geq 0 $$

Is this correct?

(3) This is my biggest problem, I have little clue on how to show this, it is clear that in $c$ it is valid. I have the feeling that using the following inequality I can get somewhere:

$$ \sup\left\{\liminf_{n\rightarrow\infty}\left(\frac{1}{k}\sum_{j=1}^k x_{n+i_j}\right) \right\} \leq f(x) \leq \inf\left\{\limsup_{n\rightarrow\infty}\left(\frac{1}{k}\sum_{j=1}^k x_{n+i_j}\right) \right\} $$

but I haven't been able to do much.

If we define $$q(x)=\sup\left\{\liminf_{n\rightarrow\infty}\left(\frac{1}{k}\sum_{j=1}^k x_{n+i_j}\right) \right\}$$

I have no trouble in noticing that:

\begin{align} p((x_2,x_3,\ldots))=p((x_1,x_2,\ldots))\\ q((x_2,x_3,\ldots))=q((x_1,x_2,\ldots)) \end{align}

If we had $p(x)=q(x)$ then it would be done, but I think this is not the case.

Any suggestions?

Answer 1

This is only about the part 3, where you want to show that for $f(x)=f(Sx)$ where $S$ denotes the shift-operator, i.e., \begin{align*} x&=(x_1,x_2,x_3,\dots,x_k,\dots)\\ Sx&=(x_2,x_3,x_4,\dots,x_{k+1},\dots) \end{align*}

Since $f$ is linear, it clearly suffices to show $f(x-Sx)=0$. So you want to show that $f(y)=0$ for any $y$ obtained as $$y=(x_1-x_2,x_2-x_3,\dots,x_k-x_{k+1},\dots)$$ from some bounded sequence $x\in\ell_\infty$.

Since $-p(-y)\le f(y) \le p(y)$, it suffices to show that $$p(y)=p(-y)=0$$ for every such $y$.

---

For this purpose, let me try to rewrite $p$ in another way.

For any finite set $F\subseteq\mathbb N$ let us denote $$M_F(x)= \limsup_{n\to\infty} \frac{\sum\limits_{j\in F} x_{n+j}}{|F|}.$$ In this way we get that $$p(x)=\inf\{M_F(x); F\subseteq\mathbb N\text{ is finite}\}.$$

Let us also have a look at a different sublinear function $$r(x)=\inf_{k\in\mathbb N}\limsup_{n\to\infty} \frac{x_{n+1}+\dots+x_{n+k}}k.$$ To relate this in some way to $p(x)$ we may notice that this can be also written as $$r(x)=\inf\{M_F(x); F=\{1,2,\dots,k\}\text{ for some }k\}.$$

After the rewriting, we can see immediately that $$p(x)\le r(x).$$

It should not be very difficult to check that in fact we have $$-r(-x) \le -p(-x) \le p(x) \le r(x).$$ (Similarly as for $p$, change from $r(x)$ to $-r(-x)$ basically just involves interchanging infima and suprema. By the way, $-r(-x)$ is exactly what you denote as $q(x)$ in the current revision of your question.)

---

So now it suffices to check that $r(y)=-r(-y)=0$ whenever $y=x-Sx$, which is almost immediate, since we get $$r(y) = \inf_{k\in\mathbb N} \limsup_{n\to\infty} \frac{(x_{n+1}-x_{n+2})+\dots+(x_{n+k}-x_{n+k+1})}k = \inf_{k\in\mathbb N} \limsup_{n\to\infty} \frac{x_{n+1}-x_{n+k+1}}k = 0$$ simply by using the fact that $0\le\left|\frac{x_{n+1}-x_{n+k+1}}k\right| \le \frac{2\|x\|_\infty}k$.

---

So it seems that the above solves the part 3. But it still seems to me that this is kind of cheating or at least not what the author intended. The reason is that we could use Hahn-Banach Theorem directly with $r(x)$ to get Banach limit (as described in my answer to another question, or in this question which was shown in the sidebar among related questions). So it seems to me rather unlikely that the proof would use a more complicated function $p(x)$ when applying Hahn-Banach Theorem and then a simpler function $r(x)$ in the proof that the resulting functional has the desired property.

But I still hope that this might be, in some way, useful to get closer to the solution which was intended by the author of the hint.

Perhaps it is also interesting to mention that in a 1988 edition of the book the author chosen a different approach to prove existence of Banach limit from Hahn-Banach Theorem, see Exercise 5 on page 140. The approach given there seems to be closer to the approach described at the end of this answer.

Answer 2

Suggestion for (3): What you have to prove is not $p(x)=q(x)$ but $$p((x_2-x_1,x_3-x_2,\cdots))=q((x_2-x_1,x_3-x_2,\cdots))=0,$$ for $$f(x_2,x_3,\cdots))=f((x_1,x_2,\cdots))+f((x_2-x_1,x_3-x_2,\cdots)).$$ Write down your answer if you get it or ask for more details if you still don't understand.

Answer 3

This is actually a long comment. An easier way to produce a generalized limit $f$ is, first, to let $C$ be the vector sub-space of all $x=(x_n)_n\in l_{\infty}$ for which the Cesaro Mean: $\lim_{m\to \infty}m^{-1}\sum_{n=1}^mx_n$ exists, and let $f(x)$ be the Cesaro Mean of $x$ for each $x\in C.$

Since $|f(x)|\leq \|x\|$ for all $x\in C$ we may extend $f$ (uniquely) to a functional $f'$ on $\overline C,$ and by Hahn-Banach, extend $f'$ to $f''\in (l_{\infty})^*$ with $\|f''\|=\|f'\|=1.$

Any convergent $x=(x_n)_n$ belongs to $C$ so $f''(x)= f(x)=\lim_{n\to \infty}x_n.$

If $x=(x_n)_n\in l_{\infty}$ and $y=(x_{n+1})_n$ then the Cesaro mean of $x-y$ exists and is $ 0.$ So $x-y\in C$ and $f''(x)-f''(y)=f''(x-y)=f(x-y)=0.$