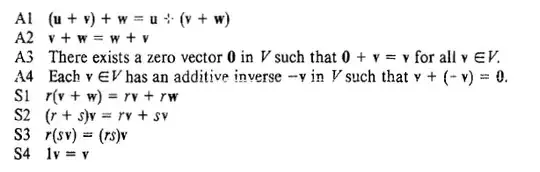-1

Show that F = $\{a + b\sqrt{3}\} | a, b \in \mathbb Q\}$ is a field under the operations + and $\cdot$, where + is given by $(a + b\sqrt{3}) +(c + d\sqrt{3}) = (a + c) + (b+d)\sqrt{3}$ and $\cdot$ is given by $(a + b\sqrt{3}) \cdot(c + d\sqrt{3}) = (ac + 3bd)+ (ad + bc)\sqrt{3}$

Do I just have to show it satisfies all the $A1 - A4, S1 - S4$ axioms?

enter image description here

For example:

$A1 = u + (v + w) = $

$$=(a + b\sqrt{3} + ((c + d\sqrt{3}) + (e + f\sqrt{3})) = (a + b\sqrt{3}) + ((c + e) + (d + f)\sqrt3{}))$$

$$= (a + c + e) + (b + d + f)\sqrt{3}$$

Also:

$$(u + v) + w = ((a + b\sqrt{3}) + (c + d\sqrt{3}) ) + (e + f\sqrt{3})$$

$$= (a + c + e) + (b + d + f)\sqrt{3}$$

Satisfies one of the eight of the axioms. Is this what I am suppose to do?

If so, I don't get how to check the scalars for example

S1: $r(u + v) = ru + rv$

$$= r((a + b\sqrt{3}) + (c + d\sqrt{3}))$$

$$= r((a+c) + (b+d)\sqrt{3})$$

Unsure what to do after this

Jyrki Lahtonen
  • 133,153
jimmy jimmy
  • 27

2 Answers2

1

Yes, you should check that it satisfies all of the field axioms.

Note that the A1−A4, S1−S4 axioms you quote are not the axioms for a field! They are the axioms for a vector space (over an already given field). You should locate the actual list of axioms for a field. For example, there should be an axiom that guarantees the existence of multiplicative inverses. And there should not be any distinction between vectors and scalars.

Chris Culter
  • 26,806
0

The axiom you linked to are those of a vector space, not those for a field.

It is true (but it is probably not your intention) that $F$ is a vector space with scalar field $\mathbb{Q}$:
$F$ is just the $\mathbb{Q}$-span of $\{1, \sqrt{3}\}$ in $\mathbb{R}$ seen as a vector space over $\mathbb{Q}$, so $F$ is a vector subspace of this vector space.

For any two fields $F_1 \subseteq F_2$, we can check quite easily that $F_2$ is a vector space with $F_1$ as scalars: all vector space axiom are field axioms in particular, and the equations thus hold in $F_2$. (multiplicative inverses are not part of vector spaces though)

The axioms for a field $(F, +, \cdot ,0, 1)$ just say that $(F,+,0)$ is an Abelian group, and so is $(F\setminus\{0\},\cdot, 1)$ while we have the distributive law $a(x+y) = ax+ay$ to link the operations $+$ and $\cdot$.

It's clear that $F \subseteq \mathbb{R}$ with the inherited operations from $\mathbb{R}$ (we don't really have to define multiplication with a formula, as the formula just follows from $\sqrt{3}^2 =3$ and the field axioms in the reals:

$$(a + b\sqrt{3})(c + d\sqrt{3}) = \text{ (by distributivity)} =a(c+d\sqrt{3}) + b\sqrt{3}(c+d\sqrt{3}) =\\ ac + ad\sqrt{3} + bc\sqrt{3} + bd\sqrt{3}^2 = ac + (ad+bc)\sqrt{3} + 3bd$$. So the only thing to check is that $F$ is closed under inverses and this is clear as

$$\frac{1}{a + b\sqrt{3}} = \frac{a-b\sqrt{3}}{(a-b\sqrt{3})(a+b\sqrt{3})} = \frac{a}{a^2 - 3b^2} + \frac{b}{a^2-3b^2}\sqrt{3}$$

and $-(a+b\sqrt{3}) = (-a) + (-b)\sqrt{3}$, so if a number $x$ is in $F$ so is $-x$ and $\frac{1}{x}$. All other field axioms are just the same equations that hold for $\mathbb{R}$. So $F$ is just a subfield of $\mathbb{R}$.

Henno Brandsma
  • 242,131