Infinite 'hex': is a win always achievable?

Question

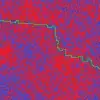
In the game hex, at least one player always wins because they can form a chain of hexagons across the board. This led me to wonder, what happens if we generalise to infinitely many points?

Specifically, if every point in a unit square (including boundaries) is coloured red or blue, does there necessarily exist a continuous function $f: [0,1] \to [0,1]\times [0,1]$ such that $f(x)$ is either

a) Always red$\space\space$ and $f(0)=(0,a), f(1)=(1,b)$ for some a,b

b) Always blue and $f(0)=(a,0), f(1)=(b,1)$ for some a,b

Furthermore, if there exists a function such that (a) is true, then does that necessarily mean there does not exist a function such that (b) is true?

(In the example, red wins with the path shown an blue loses)

My intuition tells me that this is true, but I have no idea how to begin proving it. My best idea was to colour the regions to the left and right of the square red. Then anything connected to this red region is marked green. If the other side is connected to this then we are done. Otherwise, take the points along the boundary of this green region. They must be blue otherwise there exists a point closer to the region that is blue (by definition of the green region). Hence this boundary reaches all the way down to the bottom and we are done. But I'm not sure if this green region is well-defined or anything and have no idea how to show that it is.

(Also, I've got no idea what tag(s) to put on this, sorry)

Answer 1

No. In fact, it is possible to color the entire unit square red and blue so that there is no nonconstant continuous function $f:[0,1]\to[0,1]\times[0,1]$ whose image is entirely one color. The key observation is that the image of any such nonconstant function is a closed subset of $[0,1]\times[0,1]$ of cardinality $\mathfrak{c}$, and there are only $\mathfrak{c}$ such closed subsets. You can then construct a coloring by transfinite induction so that each such set has both a red point and a blue point.

In detail, let $(X_\alpha)_{\alpha<\mathfrak{c}}$ be an enumeration of all the closed subsets of $[0,1]\times[0,1]$ of cardinality $\mathfrak{c}$. We define sequences $(r_\alpha)_{\alpha<\mathfrak{c}}$ and $(b_\alpha)_{\alpha<\mathfrak{c}}$ by induction. Having defined $r_\beta$ and $b_\beta$ for all $\beta<\alpha$, define $r_\alpha$ and $b_\alpha$ to be two distinct points of $X_\alpha$ which are not equal to $r_\beta$ or $b_\beta$ for any $\beta<\alpha$. This is possible since we have chosen fewer than $\mathfrak{c}$ points so far, and $X_\alpha$ has cardinality $\mathfrak{c}$.

We thus obtain two disjoint sets $R=\{r_\alpha\}_{\alpha<\mathfrak{c}}$ and $B=\{b_\alpha\}_{\alpha<\mathfrak{c}}$ which each intersect every $X_\alpha$. Color all the points in $R$ red, and all the points in $B$ blue, and all the points that are in neither $R$ nor $B$ however you want. Then neither the red points nor the blue points contain any $X_\alpha$, and thus neither contains the image of a nonconstant continuous function $f:[0,1]\to[0,1]\times[0,1]$.

---

However, it is true that at most one of your conditions (a) and (b) are true. See this answer to an earlier question for a proof. (The proof there assumes the endpoints of the paths are the corners of the square, but a similar argument works in general. Or, you can apply a homeomorphism of the square that sends the endpoints of the paths to the corners.)

Answer 2

Color $(x,y)\in[0,1]^2$ red if $x=0$ or $y=1/2\cdot\sin(1/x)$. Color everything else blue. There are no paths of either color connecting its respective edges.

Note that the red path does not "reach" the line $x=0$. See also this post and the counterexample in the answers: "Intermediate Value Theorem" for curves

Answer 3

Okay, thinking about it more has gotten me this answer:

Consider the colouring:

$(x,0)$ is always blue

For each natural number n,

$(\frac{1}{n},y)$ is blue iff $\frac{1}{n}\leq y$, and everything else is red.