asymptotic behavior of $\displaystyle{\sum_{r = 0}^k} { 2k - r \choose k} x^r $ for large $k$

Question

Problem

This problem comes from the partition function $Z( n, r )$ in this question. I want to analyze the large $k$ behavior of \begin{equation} f(k) = \sum_{r = 0}^k { 2k - r \choose k} x^r \end{equation} For example, \begin{equation} \sum_{r =0}^k { 2k - r \choose k} 2^r = 4^k \end{equation}

A more specific question would be the limit as a function of $x$ \begin{equation} \lim_{k\rightarrow \infty} \frac{\ln f(k)}{k} \end{equation}

One can assume $x > 0$ or even $x > 1$. I'm interested at the point $x = 3$.

---

A preliminary analysis shows that \begin{equation} \sum_{r=0}^{\infty} { 2k -r \choose k } x^r = { 2k \choose k} {}_2F_1( 1, -2k;-k; x ) \end{equation} then the problem reduces to the analysis of the Gauss hypergeometric function.

---

Update 1: numerical data

I calculate the results for $x = 0.1$ to $10$ and $k$ up to $25$

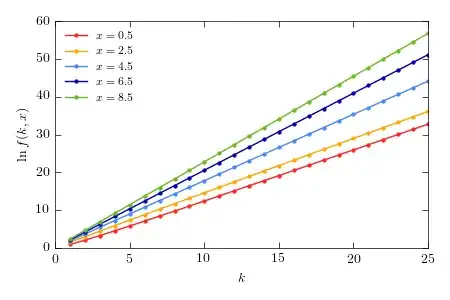
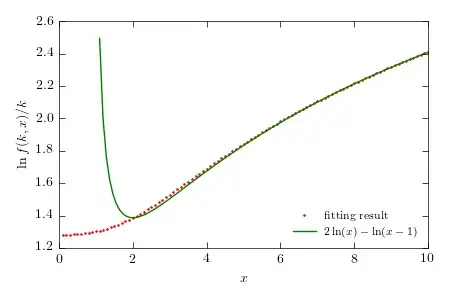
$\ln f( x, k )$ vs $k$ is pretty much on the straight line even for $k$ of order $10$.

Then I fit the curve (in range $k \in [15, 25]$) and compare the slope with the result from @ThomasAndrews

Based on this finite size numerical calculation, we can see that for $x> 4$, $2\ln x - \ln( x- 1)$ is a very accurate estimation. It is actually the exact answer( see the error estimation by @ThomasAndrews ).

However, the error term can not be improved, because the data in range $[2,4]$ is slightly above $2\ln x - \ln( x- 1)$. The estimation doesn't work for $k < 2$.

---

[2017-09-07]Update

Following @ThomasAndrews, we should analyze the scaling behavior of \begin{equation} f( k, x ) = x^k \sum_{r=0}^{k} { k + r \choose r } x^{-r} \quad x \ge 2 \end{equation}

I here present a slightly different break up.

Using Pascal's rule for binomial coefficients \begin{equation} { k + r \choose r} = { k - 1 \choose 0} + { k \choose 1 } + \cdots + { k+r - 1 \choose r } \end{equation} we have \begin{equation} \begin{aligned} f(k,x) = x^k\Bigg\{ &\left[ { k - 1 \choose 0} + { k \choose 1 } + \cdots + { 2k - 1 \choose k } \right] \frac{1}{x^k} \\ +&\left[ { k - 1 \choose 0} + { k \choose 1 } + \cdots + { 2k - 2 \choose k-1 } \right] \frac{1}{x^{k-1}}\\ +\vdots &\\ +&\left[ { k - 1 \choose 0}\right] \frac{1}{x^0} \Bigg\} \\ \end{aligned} \end{equation} Summing along the vertical lines to get a recursive relation \begin{equation} \begin{aligned} \frac{f(k,x)}{x^k} &= \frac{x}{x - 1}\left[ (1 - x^{-k-1}){ k - 1 \choose 0} + x^{-1} ( 1 - x^{-k}){ k \choose 1 } + \cdots + x^{-k}( 1 -x^{-1} ){ 2k - 1 \choose k } \right] \\ &= \frac{x}{x - 1} \left[ \sum_{r =0 }^{k-1} { k - 1 + r \choose r } x^{-r} + x^{-k}{2k - 1 \choose k } - x^{-k-1} { 2k \choose k } \right]\\ &= \frac{x}{x-1} \frac{f( k-1, x ) }{x^{k-1}} + \frac{x - 2}{x-1} x^{-k} { 2k - 1 \choose k } \quad k \ge 1\\ &= \left( \frac{x}{x - 1}\right)^k \left[ f(0,x) + \frac{x - 2}{x-1} \sum_{r=1}^{k} \left( \frac{x^2}{x - 1}\right)^{-r} { 2r - 1 \choose r } \right] \end{aligned} \end{equation}

Therefore \begin{equation} f(k,x) = \left( \frac{x^2}{x - 1}\right)^k + \frac{x - 2}{x-1} \left( \frac{x^2}{x - 1}\right)^k \sum_{r=1}^{k} \left( \frac{x^2}{x - 1}\right)^{-r} { 2r - 1 \choose r } \end{equation}

A consistency check is \begin{equation} f( k, 2 ) = 4^k \rightarrow \text{correct} \end{equation}

For general $x > 1, x \ne 2$, we have $\frac{x^2}{x - 1} > 4$, which is in the convergence range of the series \begin{equation} \sum_{r=0}^{\infty} { 2r \choose r } x^r = \frac{1}{\sqrt{ 1- 4x} } \quad |x| < \frac{1}{4} \end{equation}

Consequently, we can use this generating function to approximate the second term of $f$ (the error is $o(1)$ because of the convergence of the series), \begin{equation} \begin{aligned} f( k ,x ) &=\left( \frac{x^2}{x - 1}\right)^k + \frac{1}{2} \frac{x - 2}{x-1} \left( \frac{x^2}{x - 1}\right)^k \sum_{r=1}^{k} \left( \frac{x^2}{x - 1}\right)^{-r} { 2r \choose r } \\ &\sim \left( \frac{x^2}{x - 1}\right)^k + \frac{1}{2} \frac{x - 2}{x-1} \left( \frac{x^2}{x - 1}\right)^k \left( \frac{x}{|x-2|} - 1 \right) \\ &= \left( \frac{x^2}{x - 1}\right)^k + \frac{1}{x-1} \left( \frac{x^2}{x - 1}\right)^k \quad x > 2 \\ &= \frac{1}{x} \left( \frac{x^2}{x - 1}\right)^{k+1} \end{aligned} \end{equation}

We conclude that \begin{equation} \label{eq:Z_N-asymp} \lim_{k \rightarrow \infty} \frac{\ln f(k,x)}{k} = 2\ln x - \ln ( x+ 1 ) \quad x \ge 2 \end{equation}

I'm not sure why the fitting result is a bit off the theoretical line in $[2,4]$.

---

Thanks for your attention.

Answer 1

An upper bound, and a lower bound when $x>4$.

Assuming you mean $x^r$ rather than $x^{k}$, then you get:

$$\sum_{r=0}^{k}\binom{2k-r}{k}x^r = \sum_{s=0}^{k}\binom{k+s}{k}x^{k-s}=x^k\sum_{s=0}^{k}\binom{k+s}{k}x^{-s}$$

Now, $$\sum_{s=0}^{\infty}\binom{k+s}{k}y^s =\frac{1}{(1-y)^{k+1}}$$

for $|y|<1$.

So, when $x>1$, letting $y=\frac{1}{x}$, you get $f(k)\leq x^k\frac{1}{\left(1-\frac{1}{x}\right)^{k+1}}= \frac{x^{2k+1}}{(x-1)^{k+1}}$, or:

$\log f(k)\leq (2k+1)\log x - (k+1)\log(x-1)$ and thus:

$$\limsup_{k\to\infty}\frac{\log f(k)}{k}\leq 2\log(x)-\log(x-1)$$

The error function:

$$E_k=\frac{x^{2k+1}}{(x-1)^{k+1}}-f(k)=\sum_{s=1}^{\infty}\binom{2k+s}{k}x^{-s}$$

We can note that $\binom{2k+s}{k}<\binom{2(k+s)}{k+s}$ and get:

$$E_k<x^{k}\sum_{t=k+1}^{\infty} \binom{2t}{t}x^{-t}<x^{k}\left(\frac{1}{\sqrt{1-4/x}}-1\right)=\frac{4x^{k}}{\sqrt{x^2-4x}+x-4}=O(x^{k-1})$$

when $x>4$.

I think that means, when $x>4$, that $\lim_{k\to\infty}\frac{\log f(k)}{k}=2\log(x)-\log(x-1)$.