Is there any formula for partial sum of 2-harmonic series?

Question

Since $\sum_{i\ge 1}1/i^2$ converges, I wonder if there is any partial sum formula for it? Say $f(k)=\sum_{1\le i\le k} 1/i^2$ or $g(k)=\sum_{i\ge k} 1/i^2$ or at least an asymptotical one when $k$ is large enough?

Answer 1

One can come up with a decent asymptotic formula for $\sum_{i\geq k} 1/i^2$ by interpreting it as an approximation of the integral $\int_{k-1}^\infty 1/x^2 \,dx$.

Indeed, approximating the integral with the trapezoidal rule we have $$ \int_{k-1}^\infty \frac{1}{x^2}\,dx \approx \frac{1}{2(k-1)^2} + \sum_{i\geq k} \frac{1}{i^2}. $$ Before continuing let's analyze the error in the approximation. The right-hand side is the exact value of the integral of a piecewise linear approximation to $\frac{1}{x^2}$. The error in the linear approximation at a given point goes as $\frac{1}{x^4}$, and the integral of that goes as $k^{-3}$.

Now we can compute the exact value of the left hand side as $\frac{1}{k-1}$. Thus we arrive at the formula $$ \sum_{i\geq k}\frac{1}{i^2} = \frac{1}{k-1} - \frac{1}{2(k-1)^2} + O(k^{-3}). $$

In particular, using the fact that $\sum_{i=1}^\infty 1/i^2 = \pi^2/6$, we can also write $$ \sum_{i=1}^k\frac{1}{i^2} = \frac{\pi^2}{6} - \frac{1}{k} + \frac{1}{2k^2} + O(k^{-3}). $$

EDIT:

After some googling for higher-order terms, I found the following expansion for the sum based on the Euler-Maclaurin formula: $$ \sum_{i=1}^k \frac{1}{i^2} \approx \frac{\pi^2}{6} - \frac{1}{k} + \frac{1}{2k^2} - \frac{1}{6k^3} + \frac{1}{30k^5} - \frac{1}{42k^7}. $$

EDIT 2:

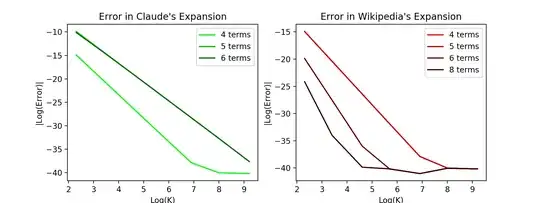
Since Claude's answer above has an expansion that disagrees with the one I found on Wikipedia, I thought I should numerically test which is correct. It turns out that Wikipedia's expansion is the correct one, as the following plots demonstrate:

I can provide the code that produced these plots if someone wants to double check.

Answer 2

You could use the fact that $$S_k=\sum_{i=1}^k\frac{1}{i^2} =H_k^{(2)}$$ where appear the generalized harmonic numbers and, for large $k$ use the asymptotics $$S_k=\frac{\pi ^2}{6}-\frac{1}{k}+\frac{1}{2 k^2}-\frac{1}{6 k^3}+\frac{1}{2 k^4}-\frac{29}{30 k^5}+\frac{3}{2 k^6}+O\left(\frac{1}{k^7}\right)$$ For example, using $k=10$ (which is not large at all) the direct summation would give $\frac{1968329}{1270080}\approx 1.54977$ while the above expansion would lead to $\frac{\pi ^2}{6}-\frac{570749}{6000000}\approx 1.54981$.

Concerning the second one, we can write $$\sum_{i=k+1}^n\frac{1}{i^2}=\sum_{i=1}^n\frac{1}{i^2}-\sum_{i=1}^k\frac{1}{i^2}=S_n-S_k$$ and reuse the above expansion. For example, using $k=10$ and $n=20$, the direct summation would give $\frac{100571322842761}{2167695039654144}\approx 0.0463955$ while using twice the above expansion would lead to $\frac{17801029}{384000000}\approx 0.0463568$.

Edit

For sure, as felipeh did in his/her answer, it would be better to use Euler-Maclaurin Summation Formula (see here) (rather than the Taylor expansion I used); this write $$\sum_{i=1}^k\frac1{i^2}=\frac{\pi ^2}{6}-\frac1k+\frac1{2k^2}-\frac1{6k^3}+\frac1{30k^5}-\frac1{42k^7}+\frac1{30k^9}-\frac5{66k^{11}}$$ which, for the worked examples given above, would give almost exact values.