1

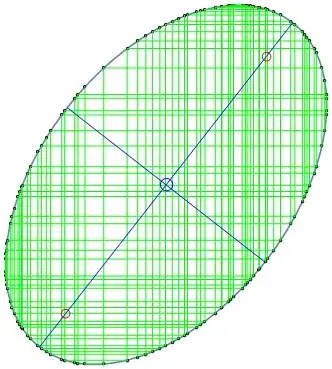
A conic goes through the points $((-1,-3), (-1,1), (0,-3), (0,2), (3,0), (3,2))$ with equation $(-5, 4, -4, 7, -4, 24).(x^2, x y, y^2, x, y, 1)=0$, that happens to be an ellipse. The ellipse passes through various other rational points, such as the following:

$((-8,-13), (-8,0), (16,5), (16,6))/5 \\ ((-14,-19), (-14,-3), (10,-19), (10,21), (18,-11), (18,21))/8 $

Here's a picture of it with various rational points connected by horizontal or vertical lines. The center is at $(5/8, -3/16)$.

ellipse

With some amount of extreme numerical hackery I found exact solutions for the major and minor axis.

Let $A$ be 4 sols of $8125 + 7500 x - 4400 x^2 - 2560 x^3 + 1024 x^4 = 0$.
Let $B$ be 4 sols of $-181561 - 9768 x - 23744 x^2 + 12288 x^3 + 16384 x^4 = 0$.

The major axis is $((A_1,B_1),(A_4,B_4))$. The minor axis is $((A_2,B_3),(A_3,B_2))$.

Why? Where the heck did those polynomials $A$ and $B$ come from that completely solve the problem? Is there some easy and elegant method for finding them? Do they have a name?

Partially caused by the paper Where is the Cone? I wondered if there was some easy way to find the cone for some random points.

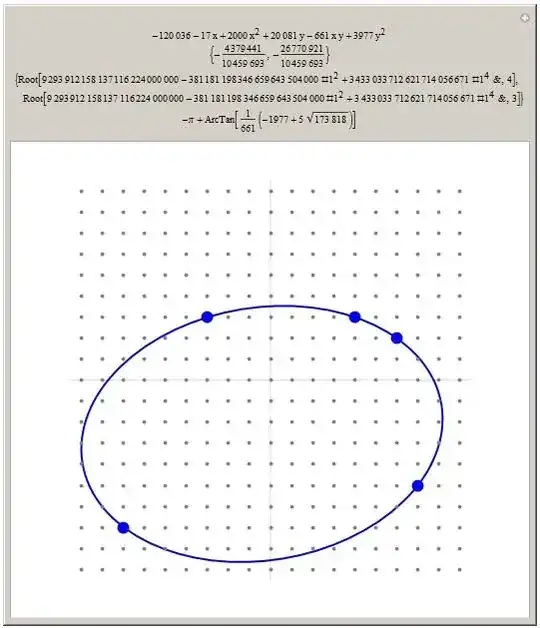
Here's five simple points leading to a scarier polynomial: $((4,3),(6,2),(7,-5),(-3,3),(-7,-7))$. Let $C$ be $$9293912158137116224000000-381181198346659643504000 x^2+3433033712621714056671 x^4 = 0$$

The lengths of the minor and major axis are $C_3$ and $C_4$.

enter image description here

Ed Pegg
  • 20,955
  • 1
    Where do you get those polynomials? How do you know what order the roots should be in? – amd Aug 25 '17 at 23:53
  • https://math.stackexchange.com/questions/1187375/given-a-drawing-of-an-ellipse-is-there-any-geometric-construction-we-can-do-to-f to find the center. Then draw a circle, calculate the line equations, find the intersections. – Ed Pegg Aug 26 '17 at 00:02
  • Sort the roots from negative to positive. – Ed Pegg Aug 26 '17 at 00:03
  • 1
    Seems like a lot of work to do to find the center analytically when you could just differentiate and solve a pair of linear equations instead. – amd Aug 26 '17 at 00:15
  • 1
    The four points represented by the intersection of two conics (the original one and the degenerate pair of lines if you know it) or indeed any two in the same pencil in general do give these degree 4 polynomials, one if you focus on the $x$-s and the other if you focus on the $y$-s. – Jan-Magnus Økland Aug 26 '17 at 06:35
  • 2
    Your equation for $B$ leads to complex solutions, please check it. – Intelligenti pauca Aug 26 '17 at 09:17
  • 1
    Presumably your polynomials find the points where the curvature is an extremum. Maximum for the major axis, minimum for the minor axis. – GEdgar Aug 26 '17 at 13:32

1 Answers1

3

Your first ellipse $−5x^2+4xy−4y^2+7x−4y+24=0$ is rotated $\theta$ from having its axes aligned with the coordinate axes $$\tan{2\theta}=\frac{2b}{a-c}=\frac{4}{-5-(-4)}=-4$$ or $\tan{\theta}=\frac14\pm\frac14\sqrt{17}.$ Using your center $(\frac58,−\frac3{16})$ we get the pair of lines $((\frac14-\frac14\sqrt{17})x-y-\frac{11}{32}+\frac{5}{32}\sqrt{17})((\frac14+\frac14\sqrt{17})x-y-\frac{11}{32}-\frac{5}{32}\sqrt{17})$ $=-x^2-\frac12xy+y^2+\frac{37}{32}x+\frac{11}{16}y-\frac{19}{64}.$

Now clearing denominators and using this answer we can get a degree 4 polynomial in $x$:

$$8125+7500x-4400x^2-2560x^3+1024x^4$$

Or a degree 4 polynomial in $y$:

$$165239-50568y-132544y^2+12288y^3+16384y^4$$

Added: A lex gröbner basis of the four points determine them more easily: $\langle 1024x^4-2560x^3-4400x^2+7500x+8125, 50y-64x^3+120x^2+125x-100 \rangle.$

Also the construction generalises: the general conic $$ax^2+2bxy+cy^2+2dx+2ey+f$$ has axes (found assuming an ellipse): $$(b^3-abc)x^2+(a^2c+b^2c-ac^2-ab^2)xy+(abc-b^3)y^2+(a^2e-ace-abd-cbd+2b^2e)x+(acd+abe+bce-c^2d-2b^2d)y+ade+be^2-cde-bd^2.$$

Jan-Magnus Økland
  • 5,149