How can I evaluate L.C.M for the three numbers $\;\;2,\;2.5,\;3\;\;?$
EDIT:
this is Ti89 calculator; and the answer is $15$ , why could that be possible?
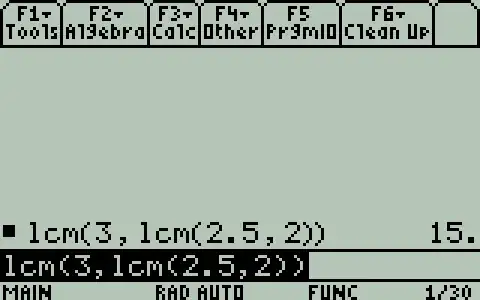
How can I evaluate L.C.M for the three numbers $\;\;2,\;2.5,\;3\;\;?$
EDIT:
this is Ti89 calculator; and the answer is $15$ , why could that be possible?

You can rewrite them as fractions:
For rational numbers, their LCM is the LCM of numerators when they're written as a fraction divided by the GCD of their denominators.
In this case, because $\gcd(1,2,1) = 1$:
$$\text{lcm}(2,2.5,3)=\text{lcm}(2,5,3)$$
Since they are all prime, the lcm is their product: $$\text{lcm}(2,5,3)=2\cdot 5\cdot 3 = 30$$
Hence, $\text{lcm}(2,2.5,3) = 30$.
There is one potentially confusing aspect of least common multiples is that the terms don't have to be integers. This is actually okay, because the least common multiple only has to be multiplied by an integer. It doesn't have to be an integer itself.
Ex. The least common multiple of $\frac 12$ and $\frac 14$ is $\frac 12$ because $\frac 12 = 1*\frac 12 = 2*\frac 14$ and so $\frac 12$ is a common multiple and it is the least (positive) common multiple.
So we need to find $k = m*2 = n*\frac 52 = p*3$ where $m,n,p$ are positive integers.
So $\frac k3 = \frac {m*2}{3}=\frac {n*5}{2*3} = p$ must be an integer so $3$ must divide $m$ and $6$ must divide $n$ and $3$ must divide $k$.
Let $m = 3m'$ and $n = 6n'$ and $k = 3k'$ and we have
$k' = 2m' = 5n' = p$
So $\frac {k'}2 = m' =\frac {5n'}2= \frac p2$ is an integer so $2$ must divide $k'$,$n'$ and $p$.
Let $k' = 2\overline k$ ,$n' = 2\overline n$ and $p = 2p'$ and we have
$\overline k = m' = 5\overline n = p'$
$\frac {\overline k}5 = \frac {m'}5 = \overline n = \frac {p'}5$ is an integer.
So $5$ divides $\overline k$, $m'$ and $p'$.
Let $\overline k = 5v; m' = 5\overline m; p'=5\overline p$ and we have
$v = \overline m = \overline p$ is an integer.
The smallest such positive integer is $v = 1$.
So $k = 3*k' = 3*2\overline k = 3*2*5 v = 3*2*5*1 = 30$.
So the least common multiple is $30$ and indeed:
$30 = 15*2 = 12*2.5 = 10*3$.
Also note $\gcd(15,12, 10) = 1$. That is not a coincidence.